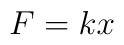Friday, December 23, 2011
Happy Anniversary
I've been too busy with my first semester of graduate school to post anything here, but I wanted to take a moment to recognize the one year anniversary of my cancer diagnosis. You can see from the picture that my hair is coming in nicely, though I have some thin spots on the sides of my head where the proton beam entered. It was a rough first semester, dealing with the fatigue that commonly follows radiation treatment, but I made it through. My last grade arrived this morning, showing that I just squeaked by the acceptable GPA. I'm optimistic that I'll be back to my old self within a few months. Once again, I'd like to thank everyone who helped me through this, but most of all, my parents. They have provided undying love and support during this difficult time, and it brings a tear to my eye every time I consider it.
Sunday, September 4, 2011
Drifting Apart
I'm finally settled here in my new home of Ann Arbor, MI, although last night I lost power in a large thunderstorm, and it's not due back until Monday night. I'm sitting in a local coffee shop with nothing much to do, so I figured I'd end my silence here by talking about an interesting feature of my new apartment.
I've found that the floor where I have my computer desk is slightly sloped, which sometimes causes my wheeled office chair to drift away from the table. What's interesting is that it only happens under certain circumstances. In order to roll back, the wheels must be pointed close enough to the direction of the slope that gravity, the force rolling it down the slope, can overcome the rolling friction created by imperfections in the wheels and the floor.
We can define an effective slope for the floor based on the direction relative to the full slope that the wheels point. If we call the full slope θ and the deviation from the straight backward direction φ, then the effective slope is
Using this, the force exerted by gravity is
where m is the mass of the chair (plus anyone in it). Frictional forces generally depend on the normal force between two surfaces. In this case, that's
Plotting these together as functions of φ gives something like
With luck, my power will be back on sooner than scheduled, but I'll try to keep posting regardless...
I've found that the floor where I have my computer desk is slightly sloped, which sometimes causes my wheeled office chair to drift away from the table. What's interesting is that it only happens under certain circumstances. In order to roll back, the wheels must be pointed close enough to the direction of the slope that gravity, the force rolling it down the slope, can overcome the rolling friction created by imperfections in the wheels and the floor.
We can define an effective slope for the floor based on the direction relative to the full slope that the wheels point. If we call the full slope θ and the deviation from the straight backward direction φ, then the effective slope is
Using this, the force exerted by gravity is
where m is the mass of the chair (plus anyone in it). Frictional forces generally depend on the normal force between two surfaces. In this case, that's
Plotting these together as functions of φ gives something like
where the green line is F and the red line is N. Anywhere the green is over the red, the chair will roll. Varying θ changes the crossing point; for sufficiently small angles, the chair will not move at all. Also note that frictional forces are usually some fraction of N, so the red line will likely be lower than shown.
With luck, my power will be back on sooner than scheduled, but I'll try to keep posting regardless...
Monday, August 22, 2011
A Tense Moment
A few days ago, I was sitting on the balcony at my parents' condo, and I noticed a water droplet on the leaf of their banana tree.
I'll be leaving for Michigan in a few days to start grad school, so there will be a pause in posting while I move in.
Seeing it got me thinking about surface tension, the force that gives it the characteristic shape that small drops have.
A simple way to think about surface tension is this: each molecule of water has a certain amount of attractive force between it and its neighbors. However, at the surface, there are no molecules on one side, so the force associated with the other molecules is stronger. Here's a diagram (from Wikipedia):
When a droplet like this sits on a solid surface, it will be spread out slightly by the force of gravity. The height is given by
where ϒ is the surface tension between air and water, θ is the angle the water's surface makes with the leaf, and ρ is the density of water. Plugging in the values we have, h = 4.1 mm. Unfortunately, my photo doesn't include any scale, so I can't check how close this is, but it sounds reasonable.I'll be leaving for Michigan in a few days to start grad school, so there will be a pause in posting while I move in.
Wednesday, August 17, 2011
Wheelchair Wheelies
Recently, my mother Sally bought her father a wheelchair. It reminded me of something I've often wondered about wheelchairs: what would it take to go up on the back two wheels? You could manage it by accelerating forward rapidly, since the wheels would essentially leave the rest of you behind, but how fast would you need to accelerate?
There are two main parameters we need to consider: y, the vertical distance between the center of mass and the rear wheel axis; and θ, the angle between those two points. They are related by
where r is the distance between the two points. Differentiating this twice gives
where dots indicate time derivatives. We know that the CM's acceleration will come from the forward acceleration of the wheels, and from gravity, so we can write
where a is the forward acceleration. Combining these gives
This is a pretty complex differential equation. I couldn't come up with an analytical solution, so I decided to do it numerically. For that though, we'll need some values. I found a helpful diagram on a Texas Accessibility Standards page, and picked out the relevant bits (measurements in mm):
I plugged in these numbers, along with a guess for a, and put it through WolframAlpha for a numerical solution. Tweaking a to find when the wheelchair lifts, I found an acceleration of about 30 m/s^2. To get a sense of scale, that's about the same acceleration involved in going 0 to 60 mph in 1 second. That would be pretty tough; I think people who do this trick press back on the seat to help.
I'm still feeling pretty crummy; yesterday I had minor surgery to have my vascular access port removed, so expect slow posting in the near future...
There are two main parameters we need to consider: y, the vertical distance between the center of mass and the rear wheel axis; and θ, the angle between those two points. They are related by
where r is the distance between the two points. Differentiating this twice gives
where dots indicate time derivatives. We know that the CM's acceleration will come from the forward acceleration of the wheels, and from gravity, so we can write
where a is the forward acceleration. Combining these gives
This is a pretty complex differential equation. I couldn't come up with an analytical solution, so I decided to do it numerically. For that though, we'll need some values. I found a helpful diagram on a Texas Accessibility Standards page, and picked out the relevant bits (measurements in mm):
I plugged in these numbers, along with a guess for a, and put it through WolframAlpha for a numerical solution. Tweaking a to find when the wheelchair lifts, I found an acceleration of about 30 m/s^2. To get a sense of scale, that's about the same acceleration involved in going 0 to 60 mph in 1 second. That would be pretty tough; I think people who do this trick press back on the seat to help.
I'm still feeling pretty crummy; yesterday I had minor surgery to have my vascular access port removed, so expect slow posting in the near future...
Friday, August 12, 2011
Suction Cups
Sorry, no clever title this time; I've been feeling pretty crummy the last few days, so I haven't been as active here as I'd like. Last time I promised a little talk about suction cups, so here we go...
Suction cups work by creating a low-pressure (or ideally vacuum) chamber, which is then maintained by the outside air pressure. We'll make a few simplifying assumptions about the suction cup: it stays perfectly conical, and its surface area remains the same.
The surface area of the cone is given by
or, solving for r^2,
Meanwhile, the volume is
Combining these and simplifying gives
Plotting this gives
Suction cups work by creating a low-pressure (or ideally vacuum) chamber, which is then maintained by the outside air pressure. We'll make a few simplifying assumptions about the suction cup: it stays perfectly conical, and its surface area remains the same.
The surface area of the cone is given by
or, solving for r^2,
Meanwhile, the volume is
Combining these and simplifying gives
Plotting this gives
The maximum on the plot will be the height with the smallest internal pressure (volume and pressure are inversely related). That means that after pressing a suction cup down to evacuate as much air as possible, pulling it up slightly will create a stronger grip.
I'm actually feeling a bit better having written this up, so maybe I just needed more brain-exercise...
Tuesday, August 9, 2011
Depressing Sleeping Arrangements
My sister Rachel has been visiting for the past few days (hence the long silence), and I gave up the guest room to her and her husband Dave. Instead, I've been staying in the living room on an inflatable mattress. I noticed that sitting on the bed makes me sink much lower than lying on it, so I thought I would look into exactly what the relationship is.
We'll assume a simple shape for the depression, like this:
Where d is the depth sunk, and A is the area that the weight is spread over. We can describe the situation with three equations:
where m is the mass of whatever is on the bed, V is the volume of air in the bed, p is the air pressure in the bed, and subscripts i and f indicate values before and after the weight is placed on the bed. Combining these and solving for d gives
A couple interesting things about this equation:
We'll assume a simple shape for the depression, like this:
Where d is the depth sunk, and A is the area that the weight is spread over. We can describe the situation with three equations:
where m is the mass of whatever is on the bed, V is the volume of air in the bed, p is the air pressure in the bed, and subscripts i and f indicate values before and after the weight is placed on the bed. Combining these and solving for d gives
A couple interesting things about this equation:
- It is possible to spread out enough that you don't sink at all.
- If you're infinitely heavy, the negative term goes to zero. At first this surprised me, since it seemed to say there was a maximum amount you could sink, but looking at the leftover term, you'd be crushing the mattress flat.
- Even with the same pressure, a larger mattress will make you sink more.
Friday, August 5, 2011
Extruded Plastic Dingus
(Title from a favorite movie of mine, The Hudsucker Proxy)
While I was visiting my brother Nate, we went to the Baltimore Farmers' Market, where a local performance group had brought a large selection of hula hoops. He felt the need to show up our mother, who had also come across a group lending out hula hoops back here in Northampton. I've never been any good with them, but I thought I'd explain a bit about how they work. I had a basic understanding, but I figured I should try to read up a bit on the details. Since I'm between schools, I no longer have access to the pricey journal databases, but I did manage to find a paper on the free physics article site, arXiv. As it turns out, the dynamics involved are rather complex, so I thought I'd try to give a basic explanation and highlight some interesting aspects.
The article presents the situation with this diagram:
The large gray circle is the hula hoop, and the smaller filled circle is your waist. The dotted ellipse represents the hip movements that keep the hoop going. The important factors that determine the movement of the hula hoop are: the friction between you and the hoop, the shape that you move your hips in, the distance that you move your hips, and the size of you and the hoop. Rather than get into the details, I'll just summarize some of the article's more interesting conclusions:
While I was visiting my brother Nate, we went to the Baltimore Farmers' Market, where a local performance group had brought a large selection of hula hoops. He felt the need to show up our mother, who had also come across a group lending out hula hoops back here in Northampton. I've never been any good with them, but I thought I'd explain a bit about how they work. I had a basic understanding, but I figured I should try to read up a bit on the details. Since I'm between schools, I no longer have access to the pricey journal databases, but I did manage to find a paper on the free physics article site, arXiv. As it turns out, the dynamics involved are rather complex, so I thought I'd try to give a basic explanation and highlight some interesting aspects.
The article presents the situation with this diagram:
The large gray circle is the hula hoop, and the smaller filled circle is your waist. The dotted ellipse represents the hip movements that keep the hoop going. The important factors that determine the movement of the hula hoop are: the friction between you and the hoop, the shape that you move your hips in, the distance that you move your hips, and the size of you and the hoop. Rather than get into the details, I'll just summarize some of the article's more interesting conclusions:
- More friction or a large hoop requires you to move your hips more
- Low friction allows you to twirl the hoop in the opposite direction that you swing your hips
- Theoretically, there are unstable solutions to the hoop's movement, meaning if you were able to get everything perfectly lined up, it would work, but in reality, you'd never manage it
Thursday, August 4, 2011
Doff Your Cap
While I was on my trip, I carried a water bottle with me everywhere to survive the heat. It had the typical screw top, and I wondered whether squeezing the bottle could cause the top to unscrew, or if the friction would be too great.
There are two forces acting on the cap when you squeeze the bottle: the increased air pressure in the bottle, and the normal force from the screw threads. We can diagram them like this:
where A is the area of the bottle cap, p is the pressure increase in the bottle, N is the normal force applied by the threads, and θ is the angle the threads are tilted at. The magnitude of N is equal to the force applied directly against the threads, so we can write
Using this, we can find the torque on the cap applied by friction.
where r is the radius of the cap, μ is the coefficient of friction, and we have assumed that A is given by the usual area of a circle.
In addition to the frictional torque, the tilt of the normal force will also apply a torque, given by
Combining these into a net torque gives, with some rearranging,
This says that any amount of pressure will cause the cap to unscrew, as long as
Plugging in a typical coefficient of friction for plastic, 0.2, gives an angle of about 11.5°. Looking at the water bottle I was using,
There are two forces acting on the cap when you squeeze the bottle: the increased air pressure in the bottle, and the normal force from the screw threads. We can diagram them like this:
where A is the area of the bottle cap, p is the pressure increase in the bottle, N is the normal force applied by the threads, and θ is the angle the threads are tilted at. The magnitude of N is equal to the force applied directly against the threads, so we can write
Using this, we can find the torque on the cap applied by friction.
where r is the radius of the cap, μ is the coefficient of friction, and we have assumed that A is given by the usual area of a circle.
In addition to the frictional torque, the tilt of the normal force will also apply a torque, given by
Combining these into a net torque gives, with some rearranging,
This says that any amount of pressure will cause the cap to unscrew, as long as
Plugging in a typical coefficient of friction for plastic, 0.2, gives an angle of about 11.5°. Looking at the water bottle I was using,
we can see that although my bottle would not work, one with only slightly steeper threads could. I think it's interesting that the pressure doesn't factor in – as long as the angle is correct, any amount of pressure can make the cap unscrew.
Tuesday, August 2, 2011
Light Rail
I have returned from my trip; big thanks to everyone who hosted me, and showed me a wonderful time. I have a couple post ideas kicking around from my travels, but I thought I'd take a minute to give a quick primer on the special relativity issues I mentioned last time.
Special relativity rests on the idea that the speed of light is constant. This may not seem like such a significant statement, but you have to consider that it means the speed is always constant. Normally if you were chasing after something, all you need to do is go faster than it, and eventually you'd catch up. However, if you tried that with light, no matter how fast you went, its speed would always appear to be the same amount faster than you. This leads to some interesting effects.
Imagine we construct a clock that uses light as its timekeeper – it contains a hollow tube with a beam of light that travels down it, bouncing off each end; each bounce is a tick. It might look something like this:
While on the train, clocks outside will appear to be running slower than my own, but since I accelerate before and after such observations, they are potentially invalid. However, someone outside looking at my clock would be correct in noting that it appears slower than theirs. Since the person outside stays still during my entire trip, their observations must be correct. If the train takes a time t according to the stationary person, then they will see a time t/γ pass on my clock. Plugging in the numbers from last time gives the 95 picosecond difference I mentioned.
Special relativity rests on the idea that the speed of light is constant. This may not seem like such a significant statement, but you have to consider that it means the speed is always constant. Normally if you were chasing after something, all you need to do is go faster than it, and eventually you'd catch up. However, if you tried that with light, no matter how fast you went, its speed would always appear to be the same amount faster than you. This leads to some interesting effects.
Imagine we construct a clock that uses light as its timekeeper – it contains a hollow tube with a beam of light that travels down it, bouncing off each end; each bounce is a tick. It might look something like this:
Now suppose we strap this clock to a rocket, and watch as it flies by. It would look something like this:
The light is still going at the same speed, but it has to travel a greater distance, so the tick that we measured earlier has been made longer by the movement. This is the relativistic effect known as time dilation. Most other interesting effects follow from similar thought experiments.
One of the important restrictions of special relativity is that it only applies in an inertial frame, that is, a perspective which is moving at a constant velocity. Technically, it doesn't quite apply to the situation I talked about last time, since my train had to accelerate up to speed, then slow down again, but we can adapt it as long as we're careful.
While on the train, clocks outside will appear to be running slower than my own, but since I accelerate before and after such observations, they are potentially invalid. However, someone outside looking at my clock would be correct in noting that it appears slower than theirs. Since the person outside stays still during my entire trip, their observations must be correct. If the train takes a time t according to the stationary person, then they will see a time t/γ pass on my clock. Plugging in the numbers from last time gives the 95 picosecond difference I mentioned.
Wednesday, July 27, 2011
Walkabout
(Another old t-shirt design. Credit goes to my dear friend Jen Trinh for the wonderful Einstein drawing.)
Tomorrow I'm heading off for a trip around the East to visit friends and family before I disappear into Michigan for grad school. I probably won't be posting anything here for about a week, but the long train ride ahead of me got me thinking about the possibility of high-speed travel to other solar-systems. I wondered about the relativistic effects of my own travel – my train ride shouldn't actually feel like 6 hours, since I'll be moving.
In special relativity, traveling at a velocity v causes time to slow by a factor of
The faster Amtrak trains average about 63 mph, giving γ = 1 + 4.4 x 10^(-15). That means that while my trip may last 6 hours, it will feel 95 picoseconds shorter than that. What a timesaver!
Tomorrow I'm heading off for a trip around the East to visit friends and family before I disappear into Michigan for grad school. I probably won't be posting anything here for about a week, but the long train ride ahead of me got me thinking about the possibility of high-speed travel to other solar-systems. I wondered about the relativistic effects of my own travel – my train ride shouldn't actually feel like 6 hours, since I'll be moving.
In special relativity, traveling at a velocity v causes time to slow by a factor of
The faster Amtrak trains average about 63 mph, giving γ = 1 + 4.4 x 10^(-15). That means that while my trip may last 6 hours, it will feel 95 picoseconds shorter than that. What a timesaver!
Monday, July 25, 2011
Zip Line and Sinker
Earlier today, Steve and I went to see Captain America. It was very entertaining, but as usual, I have a physics nitpick. In one scene, the Captain and his men ride a zip line down from a mountaintop and drop off onto a speeding train, landing with ease. It seems to me it would require an enormous height difference to achieve the necessary speed to land on the train without being thrown off.
We can find the height necessary to achieve a certain speed using energy. The kinetic energy gained by dropping a height h is
where m is the object's mass and g is the acceleration due to gravity. Meanwhile, the energy involved in traveling a velocity v is
Putting these together and solving for h gives
Given the era, I'm guessing the train was a diesel engine, so its top speed would be around 100 km/h. Plugging that into our equation gives 39 meters, or about 13 stories. Also note that this is the minimum height, since it assumes that all his downward momentum gets transferred to horizontal. If the zip line were at a 45° angle, it would require twice the height. Don't let my pedantry put you off though; it was a great movie, well worth seeing.
We can find the height necessary to achieve a certain speed using energy. The kinetic energy gained by dropping a height h is
where m is the object's mass and g is the acceleration due to gravity. Meanwhile, the energy involved in traveling a velocity v is
Putting these together and solving for h gives
Given the era, I'm guessing the train was a diesel engine, so its top speed would be around 100 km/h. Plugging that into our equation gives 39 meters, or about 13 stories. Also note that this is the minimum height, since it assumes that all his downward momentum gets transferred to horizontal. If the zip line were at a 45° angle, it would require twice the height. Don't let my pedantry put you off though; it was a great movie, well worth seeing.
Friday, July 22, 2011
Queen Kong
You may remember a post from early in my blog, when I mentioned our (relatively) new Boston Terrier, Darcy. I referred to her as a volatile dog, but didn't give any details, so I thought I might take a moment to quantify her explosive nature. She enjoys chew toys very much, but we've found that most toys can be destroyed within seconds. Squeaking weasels have been eviscerated, and bones have been chewed into shreds. The one type that has stood up to her has been the Kong, a chew toy inspired by a part of the suspension of a VW van. It's shaped as a conical tube, which she spends hours a day crushing flat, only to have it spring back. I've tried this myself (with my hands, that is) and it's impressively difficult to do, so I started wondering how many calories she was burning with this jaw exercise.
The only scale we had around was a small kitchen one that only went up to 5 kg, but if we assume the Kong follows Hooke's Law (the usual approximation for a spring) we can figure out the energy involved.
so squeezing the Kong flat (3.61 cm) requires 10.4 J, or 0.0025 Calories. It may not seem like much, but that's about equal to the energy involved in one arm-curl of an 8 pound weight. Also keep in mind that Darcy is only 18 pounds herself, so imagine lifting half your own weight. I should also note that, if anything, this is an underestimate, since it feels to me as if it gets more difficult to compress as it flattens. Further evidence that Darcy is not a dog to cross...
The only scale we had around was a small kitchen one that only went up to 5 kg, but if we assume the Kong follows Hooke's Law (the usual approximation for a spring) we can figure out the energy involved.
Measuring the larger opening closest to the camera, the difference between the uncompressed Kong (left), and the Kong compressed by 4.2 kg (right) is 0.26 cm. Hooke's Law gives the force exerted by a spring compressed a distance x as
where k is a constant that characterizes the strength of the spring. Using the information we have, k = 16,000 kg/s^2. The energy required to compress a Hooke's Law spring isso squeezing the Kong flat (3.61 cm) requires 10.4 J, or 0.0025 Calories. It may not seem like much, but that's about equal to the energy involved in one arm-curl of an 8 pound weight. Also keep in mind that Darcy is only 18 pounds herself, so imagine lifting half your own weight. I should also note that, if anything, this is an underestimate, since it feels to me as if it gets more difficult to compress as it flattens. Further evidence that Darcy is not a dog to cross...
Thursday, July 21, 2011
Raise a Glass
Last night, we drank champagne to celebrate the end of my treatment. The flutes we used got me thinking about the old trick of running a wet finger around the rim of a wine glass to make a tone. I wondered whether it would be possible to predict the frequency of the tone based on the shape of the glass. I tried it out on three different glasses:
According to Wikipedia, the resonant frequency of a cone (which we'll approximate the leftmost two glasses as) is the same as that of an open cylinder, which is given by
where n is any positive integer, v is the speed of sound, L is the length of the tube (in this case the height of the inside of the glass), and d is the diameter of the tube (in this case the diameter halfway up the glass). The rightmost glass we'll approximate as a closed cylinder, whose resonant frequency is
I tabulated the results of these equations, and the frequencies I actually measured below:
I'm impressed by how well the results fit the theory, given all the approximations involved. Even a perfect cone or cylinder would not be exactly described by the equations above, but it's nice to see that they work well on even an imperfect example.
According to Wikipedia, the resonant frequency of a cone (which we'll approximate the leftmost two glasses as) is the same as that of an open cylinder, which is given by
where n is any positive integer, v is the speed of sound, L is the length of the tube (in this case the height of the inside of the glass), and d is the diameter of the tube (in this case the diameter halfway up the glass). The rightmost glass we'll approximate as a closed cylinder, whose resonant frequency is
I tabulated the results of these equations, and the frequencies I actually measured below:
| Glass | Small Cone | Large Cone | Flute |
| n | 1 | 1 | 3 |
| L (cm) | 4.62 | 7.61 | 11.3 |
| d (cm) | 7.23 | 7.5 | 5.49 |
| Theoretical Freq. (Hz) | 1914.49 | 1416.18 | 1906.12 |
| Measured Freq. (Hz) | 1850.3 | 1548.9 | 1704.7 |
| Percent Error | 3.47 | 8.57 | 11.82 |
Wednesday, July 20, 2011
The Deed is Done
Today was the last day of my proton radiation therapy. This marks the end of my cancer treatment, though I still have a few check-ups and a lifetime of periodic MRIs ahead of me. I couldn't have made it this far without the incredible support of all my friends and family, but there are a few people that I think deserve special recognition and thanks:
- My optometrist, Brian Wadman, who first noticed my swollen optic nerve and sent me for the MRI that revealed my tumor.
- My neurosurgeon, Ziv Williams, who evidently heeded my warning that my brain is about all I have going for me.
- My oncologist, David Ebb, who planned my treatment and kept a watchful eye over me throughout the ordeal.
- My nurse, Patti Scott, who would smile and laugh with me as she drew tube after tube of blood samples from my chest-port.
- My radiation oncologist, Shannon MacDonald, who was a match for my geekiness as she explained the inner workings of the MGH cyclotron.
- My mother Sally, who kept at work during this difficult time, providing the top-notch health insurance that allowed me to be treated.
- Most of all, my father Steve, who has been my roommate, nurse, chef, personal trainer, secretary, biographer, chauffeur, and friend during the worst 7 months of my life so far.
Subscribe to:
Posts (Atom)