When we were running our Roomba this week, it seemed like it was bouncing around forever in my office, and when it finally left, came back a minute later! It made me start wondering about how the shape of the room affects the time the Roomba spends in it.
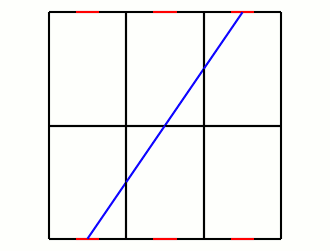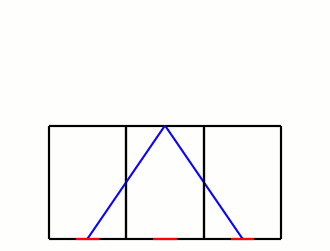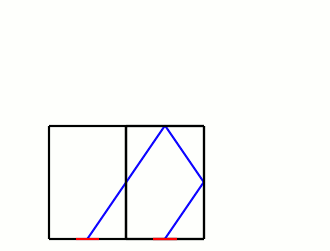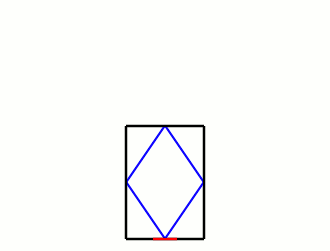
According to Roomba's marketing, it's meant to learn the layout of rooms, and trace over them efficiently, but for the purposes of a simple model, let's suppose it simply reflects off the walls like a mirror. The advantage of this behavior is that instead of worrying about the angles of the collisions, we can imagine the Roomba passing through the wall into a mirrored version of the room:
What we're looking for is the distance the Roomba travels to get from one doorway to one of the mirrored ones. If we go m doors up and n doors over, the distance will be
where l and w are the length and width of the room. The requirement for exiting the room is
where θ is the angle the Roomba enters the room, and d is the width of the door. I wasn't able to find a way to get the smallest m/n for a particular room size, so I took a large random sample, and plotted the results:
The y-axis is the distance traveled by the Roomba before exiting the room, averaged over entry angles. The color shows the length of the room, but if we average over that as well,
As the room gets larger, the distance traveled begins to taper off. This suggests the time the Roomba spends in a room is more related to the room's linear size than its area. Even that tapers, so there's evidently other factors:
It seems if I want the least interference from the Roomba, I should work inside a small box!
Sunday, April 26, 2020
Saturday, April 18, 2020
Gold Standard
My brother-in-law Alex is a fan of anime, and recently I saw him watching One Piece, a show I wrote about long ago. Since making that post, I learned about a better model for the situation, and I thought I'd revisit it, and see whether the writers know their statistical mechanics!
As a reminder, the main character in the show, Monkey D. Luffy, is described as a Rubberman. Rubber is a type of polymer, which means it consists of a chain of repeating units, called monomers. As we physicists often do, we can take the absolute simplest form of this: Each link of length a either goes up or down, with equal probability.
We can find the length of the chain and the total number of segments in terms of the number that go up, and the number that go down:
What's interesting about this model is that these equations do not specify specific links in the chain, only the total number that go up or down. That means we have a system with indistinct microstates, and entropy becomes relevant. For a system like this, the entropy is given by
What does all of this have to do with stretching though? For that, we turn to the first law of thermodynamics:
where U is the internal energy of the system, dQ is the heat added to the system, and dW is the work done on the system. For our system, we want to keep the energy constant, so we can set dU = 0, and the second law of thermodynamics gives dQ = T dS. The work done on the system is a force applied by the chain multiplied by a displacement, or dW = -f dL. The work is negative because the chain pulls in the opposite direction it's stretched. Putting all this together, we get
To find this derivative, we can solve the first 3 equations together to get S in terms of N and L. Skipping all the algebra involved, we end up with
where L0 is the length with no force applied. To find a and N, we can look back at the diagram from last time:
The sphere's mass is 29 million kilograms, and we can multiply by g to get the force. The temperature is around 300 K. We can get L from the diagram, and according to DaVinci, Luffy's unburdened arm span L0 should be the same as his height.
Rearranging the equation above,
Plugging in the values, B = 26.8 m, but A = exp(1.3729469e+29 m^-1), which is an absolutely enormous number. That suggests that for a and N to be close to the same order of magnitude, we would need around a quadrillion links, each on the order of femtometers. I thought maybe a more detailed analysis would make this situation a little more understandable, but that ball is just too damn heavy!
As a reminder, the main character in the show, Monkey D. Luffy, is described as a Rubberman. Rubber is a type of polymer, which means it consists of a chain of repeating units, called monomers. As we physicists often do, we can take the absolute simplest form of this: Each link of length a either goes up or down, with equal probability.
We can find the length of the chain and the total number of segments in terms of the number that go up, and the number that go down:
What's interesting about this model is that these equations do not specify specific links in the chain, only the total number that go up or down. That means we have a system with indistinct microstates, and entropy becomes relevant. For a system like this, the entropy is given by
What does all of this have to do with stretching though? For that, we turn to the first law of thermodynamics:
where U is the internal energy of the system, dQ is the heat added to the system, and dW is the work done on the system. For our system, we want to keep the energy constant, so we can set dU = 0, and the second law of thermodynamics gives dQ = T dS. The work done on the system is a force applied by the chain multiplied by a displacement, or dW = -f dL. The work is negative because the chain pulls in the opposite direction it's stretched. Putting all this together, we get
To find this derivative, we can solve the first 3 equations together to get S in terms of N and L. Skipping all the algebra involved, we end up with
The sphere's mass is 29 million kilograms, and we can multiply by g to get the force. The temperature is around 300 K. We can get L from the diagram, and according to DaVinci, Luffy's unburdened arm span L0 should be the same as his height.
 |
| Wikipedia |
Plugging in the values, B = 26.8 m, but A = exp(1.3729469e+29 m^-1), which is an absolutely enormous number. That suggests that for a and N to be close to the same order of magnitude, we would need around a quadrillion links, each on the order of femtometers. I thought maybe a more detailed analysis would make this situation a little more understandable, but that ball is just too damn heavy!
Saturday, April 11, 2020
Fruit Flies Like a Banana
[Explanation of title here.]
Recently, my father-in-law Scott was fashioning himself some new arrows, and I was intrigued by his set of different sized heads. He told me that the weight of the head has to be matched to the length and flexibility of the shaft to give the correct amount of wobble in the arrow's flight.
You may be surprised that arrows wobble at all, given phrases like "straight as an arrow," but if you sample the wealth of slow motion videos available, you can see it quite clearly (along with some flickering florescents):
The reason for this wobble is connected to the Archer's Paradox, which asks how an arrow can fly straight, when resting it against the bow naturally tilts it to the side. A diagram helps to understand:
The left image shows the arrow notched, but not yet drawn back. B is the line between the bowstring and the body of the bow, which is the direction the force will be applied. Drawing the arrow back (right image) brings it more in line with B, but it seems like the arrow must pass through the left configuration before it leaves the bow.
The answer lies in two properties of the arrow: flexibility and tip mass. Mass resists acceleration, so when the bowstring pushes at the back of the arrow, it will begin to flex at the back, rather than push the full weight of the arrow. This will produce a wave traveling through the shaft, until it reaches the tip. The metal tip is much denser than the wood or aluminum of the body, so it is more resistant to acceleration, allowing it to stay in the position in the right image above.
I was curious if I could create a simulation of an arrow in flight. The arrow would consist of a series of line segments with mass m and applied torque of
where k is the stiffness of the arrow. This is a simple angular spring force, using the relative bend from one segment to the next. To represent the pressure of the bowstring, we can put a force on the first segment pointing forward that tapers off over time. Since the arrow is at an angle, this force will apply a torque, along with moving the arrow forward. We represent the tip by giving the last segment a larger mass than the others. Here's one example of this model:
We can try a set of different values for the tip mass and the stiffness, and look at the x-position of the arrow at the end, i.e. how straight the arrow flew:
While we can definitely see a relationship between the mass and the stiffness, there are some flaws in this model. For one thing, that plot shows k over 3 orders of magnitude, while mass is only varying by 0.005. It's also really slow, so I may not have run out the simulations long enough to get a good measure of the accuracy. Feel free to take a look, and make improvements!
Recently, my father-in-law Scott was fashioning himself some new arrows, and I was intrigued by his set of different sized heads. He told me that the weight of the head has to be matched to the length and flexibility of the shaft to give the correct amount of wobble in the arrow's flight.
You may be surprised that arrows wobble at all, given phrases like "straight as an arrow," but if you sample the wealth of slow motion videos available, you can see it quite clearly (along with some flickering florescents):
The reason for this wobble is connected to the Archer's Paradox, which asks how an arrow can fly straight, when resting it against the bow naturally tilts it to the side. A diagram helps to understand:
 |
| Wikipedia |
The answer lies in two properties of the arrow: flexibility and tip mass. Mass resists acceleration, so when the bowstring pushes at the back of the arrow, it will begin to flex at the back, rather than push the full weight of the arrow. This will produce a wave traveling through the shaft, until it reaches the tip. The metal tip is much denser than the wood or aluminum of the body, so it is more resistant to acceleration, allowing it to stay in the position in the right image above.
I was curious if I could create a simulation of an arrow in flight. The arrow would consist of a series of line segments with mass m and applied torque of
where k is the stiffness of the arrow. This is a simple angular spring force, using the relative bend from one segment to the next. To represent the pressure of the bowstring, we can put a force on the first segment pointing forward that tapers off over time. Since the arrow is at an angle, this force will apply a torque, along with moving the arrow forward. We represent the tip by giving the last segment a larger mass than the others. Here's one example of this model:
We can try a set of different values for the tip mass and the stiffness, and look at the x-position of the arrow at the end, i.e. how straight the arrow flew:
 |
| (I could not convince PyPlot to show the tick labels properly) |
Tuesday, April 7, 2020
By Hook or By Crook
[Title from the opening of The Prisoner.]
Marika and I are back at her parents' house until we move to my next postdoc, and I've noticed something about the clock/timer on their stove. If I stand too close, the curve of the front cover blocks the tops of the digits:
Generally I'm able to read the time while only seeing the bottoms of the digits, and it got me wondering about the amount of information carried in each segment.
Digital clocks use 7-segment LEDs, which are laid out like this:
We can make a table of the segments used for each digit:
Now we can imagine removing one or more columns from that table, and see which digits are still distinguishable. I put together a Python script to try out all the possibilities, but I struggled to find a good way to show all 126 of them. I settled on an animated GIF:
You can think of the red cells as ones that are known to be blocked, or burnt out. The list at the bottom shows the digits that remain unique. Interestingly, the lower-right cell is used in all digits except 2, so as long as that one works and is off, we know the digit is 2.
Turning to the situation above, the available digits are fairly slim:
However, since this is a clock/timer, we know the digits will be changing sequentially. For half of the possible digits, we only need to wait for at most the next one to be on a known value.
Marika and I are back at her parents' house until we move to my next postdoc, and I've noticed something about the clock/timer on their stove. If I stand too close, the curve of the front cover blocks the tops of the digits:
Generally I'm able to read the time while only seeing the bottoms of the digits, and it got me wondering about the amount of information carried in each segment.
Digital clocks use 7-segment LEDs, which are laid out like this:
 |
| Wikipedia |
| a | b | c | d | e | f | g | |
| 0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 1 | ✓ | ✓ | |||||
| 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 3 | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 4 | ✓ | ✓ | ✓ | ✓ | |||
| 5 | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 6 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 7 | ✓ | ✓ | ✓ | ||||
| 8 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| 9 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Now we can imagine removing one or more columns from that table, and see which digits are still distinguishable. I put together a Python script to try out all the possibilities, but I struggled to find a good way to show all 126 of them. I settled on an animated GIF:
You can think of the red cells as ones that are known to be blocked, or burnt out. The list at the bottom shows the digits that remain unique. Interestingly, the lower-right cell is used in all digits except 2, so as long as that one works and is off, we know the digit is 2.
Turning to the situation above, the available digits are fairly slim:
However, since this is a clock/timer, we know the digits will be changing sequentially. For half of the possible digits, we only need to wait for at most the next one to be on a known value.
Subscribe to:
Posts (Atom)