When we were running our Roomba this week, it seemed like it was bouncing around forever in my office, and when it finally left, came back a minute later! It made me start wondering about how the shape of the room affects the time the Roomba spends in it.
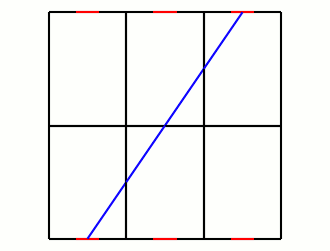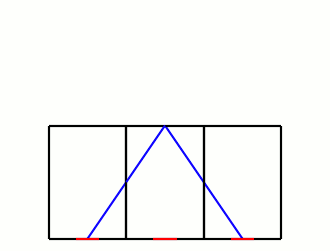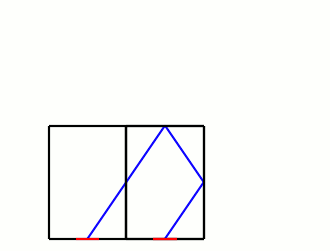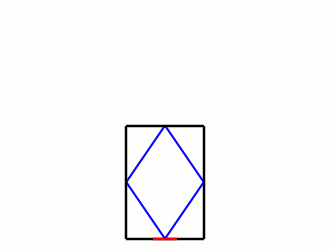
According to Roomba's marketing, it's meant to learn the layout of rooms, and trace over them efficiently, but for the purposes of a simple model, let's suppose it simply reflects off the walls like a mirror. The advantage of this behavior is that instead of worrying about the angles of the collisions, we can imagine the Roomba passing through the wall into a mirrored version of the room:
What we're looking for is the distance the Roomba travels to get from one doorway to one of the mirrored ones. If we go m doors up and n doors over, the distance will be
where l and w are the length and width of the room. The requirement for exiting the room is
where θ is the angle the Roomba enters the room, and d is the width of the door. I wasn't able to find a way to get the smallest m/n for a particular room size, so I took a large random sample, and plotted the results:
The y-axis is the distance traveled by the Roomba before exiting the room, averaged over entry angles. The color shows the length of the room, but if we average over that as well,
As the room gets larger, the distance traveled begins to taper off. This suggests the time the Roomba spends in a room is more related to the room's linear size than its area. Even that tapers, so there's evidently other factors:
It seems if I want the least interference from the Roomba, I should work inside a small box!





No comments:
Post a Comment