Triboelectric Slide

Recently I've been thinking back to my time at Eaglebrook, which I attended for 7th-9th grade (more on why it's on my mind at a later date). A memory surfaced that seemed ripe for analysis here: I was on the Ultimate Frisbee team, and there was one day that our practice was rained out, so we went to exercise in the hockey rink, which had been drained for the Spring. We decided to play blob tag: In case it's been too long since grade school, any time the person who's It tags someone, they join hands and become a bigger It. By the end of the game, most of the players are joined in one long It chain. We realized that by playing in the hockey rink, we could stretch from one wall to the opposite and simply walk toward the remaining players, who were now cornered. The kids on the ends of the chain ran their fingers along the walls of the rink, and after a few seconds, a massive static discharge traveled down the line from each end, meeting at our coach in the center, who fell to his knees in pain, clutching his arms!

Naturally, thinking of this made me wonder whether I could model the situation. Static electricity is typically caused by the triboelectric effect, in which charges transfer between materials in contact due to differences in the energy states, though the precise mechanism is not fully understood. I decided to try modeling my situation as a circuit:

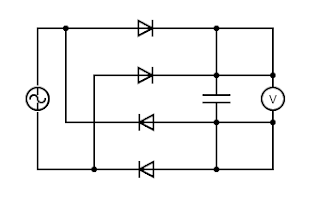
Made using circuit-diagram.org

Here we have the charged walls providing a voltage (circled arrows) and the players linked to each other (resistor Ts) and the ground (lined triangles). We can analyze this circuit using Kirchhoff's Laws: At each junction of wires, there must be a constant voltage, and all currents in and out must sum to zero. These seem simple, but when you have a tangled mess of components like this, it can get tricky. I worked out what I thought was the answer, doubted myself, worked it out again and got the same thing, so I think this is right. If the static from the wall produces a current I with a voltage V, then the nth person from the wall will discharge a current of

This seems to suggest that the current decreases as we move away from the wall, since the n(n+1) term will grow faster than the n. However, we also need to consider the charge coming from the opposite wall. For N people in the chain, the total will be

Note that we subtract the current from the opposite wall, since it's flowing in the other direction. It's a little hard to see what's going on here, so let's throw some numbers at it: The resistance of skin can vary a lot depending on how dry it is and other factors, but a typical value is 1000 ohms.

For the total current from each wall I, I found a paper on measuring the triboelectric charge transferred for different materials, which happened to include high-density polyethylene (HDPE), the substance commonly used in skating rink walls. Unfortunately, it does not have human skin, but I took their measurement of pigskin as a good representative (and appropriate for the day of the Super Bowl). The numbers they give are charge per area, but we want current, which is charge per time. We can imagine as the players walk forward dragging their fingertips along the wall, the total area will accumulate proportional to the width of the fingers contacting the wall, and the speed they're walking. Using the numbers from the paper, and assuming 1 cm width for each of 4 fingers moving against the wall at 1.5 m/s, we get (30 uC/m^2)*(4 cm)*(1.5 m/s) = 1.8 microamps.

We still need the voltage V, but we know from Kirchhoff's Laws all the individual currents need to sum to I, so we can sum In from 1 to N, set it equal to I, and solve for V:

Now we can plug this into the equation for the current discharge to see what each player gets:

Due to the flip in direction of the current at the far wall, it remains true that the highest current is on the ends, and the person in the center should feel nothing, so already things are looking bad for this model. What about the overall magnitude of the current?

According to OSHA, you start to feel a tingle around 1 milliamp, but below this would not notice anything. Our current is 5x smaller, so certainly not enough to cause the effects I saw (and felt myself)! I think one of the problems with this analysis may be the assumption of continuous discharging – If we let the charge build up for some time before being released, it could generate significantly higher currents, and may not be perfectly symmetric. Perhaps some intrepid Eaglebrook students can repeat the experiment, and gather more data!

The Fault in Our Ground

Yesterday, we took the camper to refill propane and get it cleaned. When we came back to our site, and plugged in to the campground power, we found nothing was flowing! We tried a couple ideas to solve it, but we were exhausted and it was already dark, so we turned up the (newly filled) propane heat and went to sleep. This morning, after much more troubleshooting, we discovered the issue was the ground fault circuit interrupter (GFCI), which we had tried the previous night, but hadn't performed the necessary reset steps correctly. I thought I'd get some good out of the frustrating experience, and write a post on GFCIs.

Humans are essentially big bags of salty water, which makes us good at conducting electricity. Unfortunately, letting anything more than around 100 milliamps flow through us can be fatal. The 120 volts that the US uses for mains power can create this much current under the right conditions, so we need safety mechanisms to prevent it.

A "ground fault" refers to the amount of outgoing current not matching the amount of current returning to the power source, meaning that charge is finding another path to flow down. We can measure the current in each line using a loop of wire, which picks up the magnetic field of the moving charges and generates a voltage in the loop. If the two lines don't match, we break the circuit:

In this diagram, the green loops measure the current, and the red is the GFCI's circuitry to compare and break the connections. Initially, I had wondered how a single outlet could cut power to all outlets, but this diagram makes that clear: Typically houses are wired with a pair of lines going from the source to some endpoint, and outlets are wired across the two in parallel. However, if we can break these lines immediately after the source, none of the downstream plugs will be powered.

That brings us to our issue: Once the GFCI is tripped, what do you do next? Typically, GFCIs have two buttons on them, Test and Reset. The test button will artificially pop the breakers so you can ensure they work, but critically, this requires having power. Once we had discovered the power wasn't working, we disconnected from the line in case whatever unknown problem was a fire risk. The real issue though was that to reset the GFCI, you need to push those breakers back in. They're designed to stop power within a tenth of a second, so they use powerful springs to open the connection quickly. That means you need to push a tiny button deep inside the outlet with incredible force, something we were incapable of doing last night! Thankfully in the morning we worked it out, and our power is back on without any expensive fix.

That's Mow Like It!

[Title shamelessly stolen from The Simpsons.]

Yesterday, I mowed the lawn with our fancy electric mower, which has a nice speed control for its self-propelling feature. It got me wondering though: What's the most efficient speed to mow the lawn? The blade is constantly running, so it seems like finishing the lawn as quickly as possible would be best, but then the drive is using more power. Is it better to use a lower drive speed to save energy?

I couldn't find many details on the battery/motor specifications, so we'll have to make some assumptions: I'm not sure how the variable drive speed/constant blade speed would work with a single motor, so I'm betting there's two. That means we can split up the power use like this:

The manual gives a couple different cases for battery life, but since it applies to both the self-propelled and meatbag-propelled models, I'm guessing it's assuming the drive is off, so that only tells us about the blade power. For the drive power, I decided the closest analogy would be an electric golf cart. We can look at its power use, then scale it by the ratio of weights and speeds. This model uses 2.6 kW to haul 270 kg at 15 mph. The mower weighs 28.4 kg with a top speed of 3.1 mph, so a rough approximation for power would be 57 Watts.

Now there's the question of efficiency: When we put power into an electric motor, how well does it put that power back out? Luckily, I found a great DoE paper on how the efficiency changes with percent of maximum power. I grabbed a couple points from Figure 1 and did a rough curve fit:

where e is the output efficiency and L is the fractional load.

For the "light load" case, the manual says the battery, which holds 7.5 Amp-hours of charge and runs at 56 Volts, will last for 60 minutes. After a bit of computation, that means the blade is using 420 Watts. Now we need to know how long it takes to mow the lawn, depending on the speed. Using a tool like this, we can find the total area of the property, 1065 m^2, and the total area of the house, 246 m^2, to find the approximate area of the lawn, 819 m^2. The mower is 0.53 m wide, so the minimum total distance it would have to travel is 1545 m.

We now have a long chain of relationships we can put together. The total energy used is

where P is the power, and t is the total time. The time it takes to mow is

where d is the distance, and v the velocity, which in turn is

The power, from earlier, is

The equation we get from putting all these together is a bit involved, so I just made a plot instead:

The battery's total capacity is about 1,500 kJ, so even at the slowest speed we're well within a single charge. I was hoping using the motor efficiency curve would give a more interesting result than "go as fast as you can," but since the maximum load is most efficient, that's the result. Maybe my next step will be figuring out how to balance the exertion of following the mower with the time out in the hot sun!

Loops on the Ground

This week in one of my group meetings, a colleague presented her work on identifying and eliminating ground loops. I had never heard of the phenomenon, but it's an interesting pitfall in circuit design. When we talk about voltages, we always need some reference point – Voltage isn't an absolute value, but the difference between two points. When designing a circuit, it can be useful (and safer) to have a connection that can give or take current freely. This lets you get rid of excess positive or negative charges, like static electricity, that otherwise could damage components. This is why modern outlets have 3 connections: positive, negative, and ground.

When we connect devices together though, a problem can arise:

Here we have two components, both connected to AC outlets (+, –, GND). One of them sends a signal to the other. Since voltage is a difference, we need a second connection as reference, so we use the ground wire from the outlets. Now we have a loop of wire though – A loop is a type of antenna, which can pick up signals.

According to this article, the voltage produced by a small-loop antenna is

where N is the number of loops (1 in this case), A is the area, λ is the wavelength, E is the electric field strength, and θ is the angle between the loop and the signal. This article, about honeybee exposure to RF signals, gives the maximum electric field strength measured as 0.226 V/m. FM radio signals go up to about 200 MHz, or a wavelength of 1.5 m. If the area of the loop is 0.1 square meters, or about 32 cm per side, we can get as much as 95 mV of interference, easily enough to throw off a delicate measurement!

Marika's parents are visiting us right now, so I asked my engineer father-in-law Scott if he was familiar with ground loops. He related an interesting experience: He used to have a phone that he would plug into his car power, and an audio jack to play music through the speakers. The power and audio shared a ground connection, resulting in a loop that would add static noise on top of anything he played!

Riding a Charger

In high school, I got interested in electronics tinkering through the blog Hack-a-Day. I haven't done much myself for many years, but I still read the blog, and last week there was a post that seemed ripe for physics analysis:

The setup is that each player has a button they can press and release. While the button is pushed, a capacitor is charged by a voltage source, and when it's released, the capacitor switches to power a motor that drives the horse. You can see the full plans here, but this is a simplified version of the circuit:

Made using www.circuit-diagram.org

In the state shown above, the voltage source (V) begins to charge the capacitor (C). At first, this would act like a short circuit, so we add a resistor (R) to limit the current flow. For this type of circuit, the charge on the capacitor is given by

The voltage over a capacitor is proportional to the charge stored in it, so as the capacitor charges up, it pushes back more and more on the voltage source, which slows the charge that's added. That leads to an asymptotic behavior:

When the button is released, the switch in the diagram above flips to the other side of the circuit, and the capacitor begins discharging through the motor. This acts like a resistor, but converts the charge flowing through it to motion, driving the horse. Once again, we have an asymptotic relationship, since as the charge flows out of the capacitor, it can't push as strongly:

Here, Q0 is the amount of charge we put on in the first step. This is similar to the plot above, but decaying to zero:

This made me curious if I could come up with the optimal strategy for getting the horse to the end as quickly as possible. That translates into the most charge in the least amount of time, or the maximum current. If we ignore the initial charge up, we can think of switching between some maximum and minimum charge:

The average current through the motor over one cycle is

where tC and tD are the charge and discharge times. The expressions for those are a bit ugly, so I won't write them out here. Rather than try to get the exact maximum current, we can try a variety of values for Qmin/max:

The best option appears to be keeping the capacitor at ~50% charge by rapidly flipping the switch between the two states. As with many games, the answer lies in hyperactivity!

Harry Nyquist the Scientist (Harry! Harry! Harry!)

Ok, doesn't quite scan, so I guess he's not destined for TV stardom, but one of his ideas is at the core of this week's post. Last week, I was talking to my parents over Facetime and Steve, ever the stickler for visual quality, complained that my lights appeared to be flickering:

Looking at it from my end though, the light appeared fine. I realized that the LED bulb must be flickering (by design) at a rate higher than my eyes can perceive, but my laptop camera is recording below the Nyquist rate, causing the flickers to appear.

Before getting into that, let's talk about how LED bulbs work. LEDs require direct current (DC), while house power is alternating current (AC), so the first thing we need to do is convert between these two. Alternating current is a sinusoid, oscillating between positive and negative of a certain value:

There's an electrical component called a diode that only allows current to flow in one direction. In fact, that's the D in LED, but right now we're just talking about the regular kind of diode, not the Light Emitting ones. By arranging a few of those in a clever way, we can switch the negative part of that curve to positive:

Made with circuit-diagram.org

On the left is the AC source, and on the right is a voltmeter. The diodes in the middle only allow current to flow in the direction of the arrow. The voltmeter's output looks something like this:

This isn't ideal though, since the voltage is going all the way down to zero. We need a way to smooth out this curve. We can do that by adding a capacitor, which stores and releases charge as the voltage changes:

Now the voltage looks something like this:

Still not perfect, but it's the best we can do with something simple. Those little bumps mean the LEDs will be flickering a tiny bit, but it's at twice the rate of the original AC input. In France, this is 2x50 times per second (Hz).

The camera on my laptop captures video at about 30 frames per second. According to Nyquist, to accurately record a signal, we need to take data at twice the rate that the data changes, but that would be 200 Hz, far above what my camera is capable of. We can see why this is necessary by considering a point moving in a counter-clockwise circle:

The dot completes a cycle every 8 steps. The image on the left is sampled every step, while the one on the right is sampled every 7 steps. The slower sample rate causes the dot to appear to be moving backwards. You've probably seen a similar effect in videos which include old TVs or computers that used CRT screens. The screen appears to blink because the camera captures the screen at different points in its refresh.

That leaves us with the question of why the light doesn't blink according to our eyes. That's addressed by the flicker fusion threshold, which comes from the spectacularly-named field of psychophysics. Our eyes aren't able to perceive changes in intensity above a certain rate, instead averaging things out. For most people, it's around 80 Hz, so the LEDs easily surpass that, but the captured video is nowhere close.

Thanks for a great question/complaint Steve!