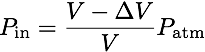I Have a Bad Feeling About This

I often have ideas for this blog that aren't quite developed enough to make a post, so I put them on a list to come back to later. This one is far from the oldest, but it is from 2015: Starkiller Base from Star Wars VII: The Force Awakens. What struck me was the details they showed:

The weapon is powered by siphoning off energy from a star, and then blasting it at a distant target. It occurred to me this week that it's actually pretty easy to figure out the energy needed to blow up a planet, and so I could assess the feasibility of doing it with power from a star. (Marika is sure I'll be put on government watch lists for talking about this.)

Planets (and stars) are held together with gravitational potential energy, which depends on the mass and the density. You can calculate it for a uniform sphere by adding up a series of concentric shells, or you can look up the answer on Wikipedia:

It's negative because gravity is an attractive force, and this represents the energy that must be overcome to scatter the planet far enough that it won't reform. For the Earth, this comes to 2.2 x 10^33 Joules, so now we need to know how much energy we can get from a star.

The Sun radiates energy at a rate of 3.846 x 10^26 Watts, or Joules/second. If the base collected the light passively, it would take about 66 days to charge up, which isn't ideal. It needs even more energy than that, given that it's able to target multiple planets at once:

Let's suppose it can absorb all the energy the star would produce over it's entire lifetime. For our sun, the estimated lifespan is 10^10 years. It probably won't have the same luminosity over its full life, but I couldn't find a simple model for how it would vary, so we'll suppose it's constant. Multiplying by the power from earlier, this gives 1.21 x 10^44 Joules, or enough to destroy 55 billion planets! Neither situation seems very practical, which may be why the Empire/First Order has so much trouble holding on to power.

The Slammer

With the warmer weather here, Marika and I have been opening up patio doors and windows to get some air moving. I've noticed though that when I go to close the front door when I'm going in or out, the amount of force I'm used to using makes the door slam. My hypothesis was that this was because in a (nearly) sealed apartment, closing the door reduces the volume of air, creating negative pressure. In an open apartment, new air flows in from the windows, but otherwise the pressure from outside stops the door from closing.

For simplicity, we'll assume the door shuts quickly enough that no air leaks around the edge. That lets us relate the angle the door has swung through to the volume of air that's been removed:

where r and h are the width and height of the door. For an ideal gas, pressure is inversely proportional to volume:

where V is the total volume of the apartment, and P_atm is the atmospheric pressure outside (and initially inside). As the door is swinging shut, the volume is increasing and the pressure is decreasing. We can multiply these quantities to find the energy needed to close the door:

Substituting in from above, this comes to

Let's get some numbers to find out how plausible this is: According to my lease, the apartment is 47.88 square meters, and this site suggests a ceiling height of 2.3 meters, which gives a volume of 110.1 m^3. This page gives the door dimensions as 0.9 x 2.15 meters. Plugging all that in, along with an angle of 90° gives 136.9 kilojoules. It's a little hard to picture an amount of energy, so we can convert it by considering the kinetic energy of the door:

We can find the door's rotational inertia I from the mass, and the dimensions from earlier. Putting everything together, the speed necessary to close the door with the resisting pressure would close it without pressure in only 7.366 milliseconds! This seems pretty extreme, but I imagine it's due to the assumption I made at the very start about no air leaking around the edges. It's impressive how much difference that bit of air can make out of a whole apartment.

Bi-Psyche-Skull

[Title thanks to the Animaniacs.]

I'm a fan of the blog Futility Closet, and a while ago their email bonus posts I subscribe to included this interesting physics problem:

I was especially curious about the angle dependency (see 4:37), so I decided to work out the mechanics.

To avoid dealing with chains and gears, let's just look at the spool shown at the same point in the video. The two forces that make it roll are the cord we're pulling, and the friction with the table:

The friction force is proportional to the normal force from the table, which is the weight of the spool, minus any vertical component of the cord force:

This frictional force applies a torque that rolls the spool to the right (clockwise), while the torque from the cord rotates the spool in the opposite direction. After a bit of algebra, the condition for rolling to the right is

Since the angles we're interested in only go between 0° and 90° (always up and right), the sine of those angles only go from 0 to 1. That means we can put limits on the pulling force to be able to choose an angle that rolls one direction or the other. The forces that allow rolling to the right are

and the forces for rolling to the left have

Some implications of this are that making the inner spool tiny always allows rolling right, but since by definition R > r, adjusting the radii can't remove the limits on rolling left. I'm a little surprised the same angle can roll left or right depending on the force. This may have to do with the fact that I have not considered whether the spool slides on the table, as well as rolling.

I scoured my apartment for something I could use to figure this out experimentally, but I couldn't find anything close enough to a spool of wire. I encourage anyone reading to try it at home and post results in the comments!

Aaron Aaronsonn Acquired an Acre of Abundant Apples

I keep a list of topics I'd like to use for these posts, and while this one is far from the oldest, it is from last fall: My friend Kevin came to visit and as a seasonal Michigan activity, he, Marika, and I went apple-picking. The orchard we went to sold bags of various sizes, and then would let you pick however many fit in the bag. Being physicists, Kevin and I began to wonder about the packing efficiency of the apples: Given the constant volume of the bag, is it better to pick more small apples, or fewer large ones?

For a given size, we want to get as many as possible into a space. This idea is usually represented with a lattice: an arrangement that repeats over some grid. Here's a pair of examples in 2D:

On the left is a square lattice, while the right is a hexagonal lattice. Our situation is 3D though, which makes things a little more complicated. If we approximate the apples as spheres, then we can use Gauss's solution for the density:

This is the density of apples inside the bag. There's a further complication though: The apples have cores that we'll be throwing away, so we have to consider the amount of each apple that the core takes up. I was surprised to find a paper studying exactly that, for the purpose of designing a mechanical coring device. They give the apple and core diameters for a few different varieties, and the relationship is roughly linear:

With the fit, we can relate the apple's diameter to its useable volume:

The total number of apples that fit in a bag is

where the brackets indicate rounding down to the nearest integer, since (hopefully) we're only picking whole apples. The total volume of useable apple then is

Below is a plot of the apple diameter vs the percentage of the bag wasted as air or core. The dotted lines represent the range of diameters from the study above, but I decided to extend the range to some more extreme values.

On both ends of the scale, our approximations begin to break down: On the left, the core shrinks faster than the useable apple, so we get down to the minimum 26% waste due to the packing inefficiency. On the right, you can't fit many 6-inch apples in a bag, so there are some sharp jumps. On the whole smaller apples are better, but in the realistic range, there isn't much difference. Clearly, further study is needed – Back to the orchard!