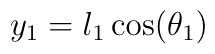Make Like a Tree and Get Out of Here

Swarthmore's Scott Arboretum traditionally gives incoming students a plant to care for in their dorms. Shockingly, the Hawaiian Schefflera I received in 2007 is still going 17 years later! Over the years as I've moved from place to place and kept the plant in different environments, I've been impressed by its ability to track the sunlight, frequently growing lopsided as it reaches toward the nearest window until I think to turn it. This has resulted in some twisting, gnarled branches:

If you've been reading this blog, you can probably guess where this is going – I was curious if I could make a simulation of my plant's heliotropic tendencies. I decided to model the plant as a collection of connected branch segments, each a fixed length and pointing at an angle relative to the vertical. At each step, we iterate over all the segments and pick an action:

• If the segment has no children, i.e. it's at the tip of a branch, we add a new segment on the end with a probability p_grow/size, where size is the number of existing segments.
• If the segment does have children, we add a new one with probability p_sprout/size.
• If neither of those occur, we adjust the angle of the branch to point closer to the sun's current position. The adjustment is proportional to how far off the angle is, how many branches are on the end of this one, and a constant stiffness for the plant.

I tried a bunch of values for the different parameters until I landed on a range that gave plants looking reasonably similar to the real thing (click to enlarge):

The numbers along the top give the stiffnesses, and the ones on the left give the sprout probability. The sun moves back and forth sinusoidally, which you can see in the snaking of the plants. I wasn't able to get my digital plants to spread as much as the analog one, possibly because I'm not accounting for the plant casting shadow on itself, but I'm still pleased with the results – The top center one seems particularly good. If you'd like to try for yourself, the code is here.

An Honest PUC

Back in January, my brother Nate got several BirdWeather PUCs, small outdoor devices that listen for bird songs, and identify the species responsible, similar to the popular Merlin phone app. He gave one to our parents, one to Marika and me, and kept one for himself. If you follow those links, you can see each PUC uploads its observations to a central server, which can be queried through an API. Nate used this to set up a daily email giving the previous day's species counts for each of our stations, and I was curious if I could apply some of the data analysis techniques I've learned to the results.

The first thing I wanted to try was identifying trends in the time of day each bird is heard. To do this, we can use an idea called data folding. This is similar to the idea of a Fourier transform, where we're dealing with periodic data, but we're only interested in a single period: 1 day. If we split our months of data into single-day segments and stack them on top of each other, we can get better statistics about when each bird is heard. There are too many individual species to look at all of them, so I considered finding a way to group them. One idea was to use their taxonomy, but depending on the level I chose, I'd get either one big group, or a group for every bird. Going back to the better statistics idea, I decided to just plot the ones with more than 200 total detections:

This is called a violin plot, often used to show statistical distributions like these. The end caps show the max/min values, and the bulges show the more frequent times. You can see that most peak around dawn hours, but a few are heard throughout the day.

In the daily emails Nate set up, I noticed that for a long time I only saw the Carolina wren show up in Florida, but then it started popping up in Massachusetts as well. I wondered if I was seeing a spring migration, so I got the data from all 3 of our stations, and looked at the number of wrens for each day:

This seems to show it was just my imagination: The wrens are much more frequent in Florida overall, and there doesn't appear to be a trend toward MA over time.

In the first plot I showed, you may have noticed the "Engine" entry. It turns out the PUC has several non-bird sounds it recognizes, and it picked up the highway traffic next door to us. I was curious to see what other non-bird detections it had made. The reported data gets a "confidence" rank based on both how close the sound was to the model, and how likely it is to hear that sound in the location. I split up the detections below on those rankings:

It's reassuring to see the few "gun" detections don't rise above uncertain, though the siren counts are quite high (and I'm assuming that refers to the emergency-vehicle type, not luring-sailors-to-doom type). Seeing these makes me curious what other sounds it can recognize. Thanks for this cool gift, Nate!

[Edit: I noticed this post is getting lots of traffic from the BirdWeather community. Maybe someone *cough*Nate*cough* shared this post there, but anyway, here's my code!]

[Edit 2: I've made a JavaScript tool that can fetch the latest data from a given station and plot histograms like the ones above.]

Dirty, Disgusting, Filthy, Lice-Ridden Boids

[Title from The Producers]

Long ago I had a screen saver with a simulation of bird flocking behavior – A group of 2000s-era 3D blocks would fly in formation, land, and take off. I was recently reminded of it, and grew curious how it was made. My best guess is that it used a model developed in 1987 called Boids. The model consists of a group of agents (boids) that each act according to a set of simple rules. In this case, the rules are

• Separation: Avoid flying into nearby flockmates
• Alignment: Fly in the same average direction as nearby flockmates
• Cohesion: Fly toward the average position of nearby flockmates

Along with these, I also included a target location that all boids want to get to. There's a lot of details unspecified here, like what "nearby" means, and how these various rules are weighted, e.g. cohesion and separation can be directly opposed at times. I looked at a couple implementations I found online, and tweaked my own model until I got reasonable looking results.

In the simulation below, the boids are all heading for the center of the map, and "nearby" covers about 1/4 of the map. I used "toroidal boundary conditions" which means if a boid goes off one edge, it wraps around to the opposite side. You can see that a few boids sometimes break out of the "nearby" region and head off on their own before rejoining:

I was pretty happy with how this worked out, but I felt like I should give it more of a physics spin. It occurred to me: What if these were relativistic boids? If they're moving at a significant fraction of the speed of light, then the observations they use to follow the rules above are based on the light arrival time, which may not reflect the current motion of a particular boid. What this amounts to is that based on the distance between two boids, their observations are delayed by a certain time. Here's what happens in that situation:

I was really surprised by the results – I expected that they would have a much harder time sticking together, since their actions would be too imprecise, but instead they show better clustering. I think this is because by staying closer, they get more up-to-date measurements, so it ends up being a positive-reinforcement.

I figured I could get a more qualitative comparison by computing some summary statistics. First I looked at the average distance between the boids at each time:

This shows the relativistic boids bunching up quickly, but then oscillating sharply around a higher value than then lowest the non-relativistic boids are able to hit. We can also look at the deviations in the boid's headings for the two cases:

This shows the relativistic boids frequently going in different directions, which we can see in the animation above: The tight grouping requires quickly changing direction to stay in one place.

I'm not sure whether any of the space organizations have plans for high-speed probe swarms, but if they do, I hope this will serve as my grant proposal!

Cyclopian Cyclones

For the past 2 weeks, I've been struggling with a question from Papou, as well as struggling with a stomach bug which probably didn't help, but I finally have an answer! Papou wondered, How does the Coriolis affect hurricanes in the northern hemisphere and what is the percentage centrifugal velocity increase/decrease at the eight points on the compass assuming the hurricane is moving directly East to West?

Coriolis force is one of the fictitious forces that appear in a rotating reference frame, along with the centrifugal and Euler forces. If you look at articles on why hurricanes spin the way they do, they'll give explanations about how the speed of the Earth's rotation varies depending on how close to the pole you are, which causes the Northern edge of the hurricane to be pushed one direction, and the Southern edge pushed the other way. This explanation makes sense, but it didn't fit with my algebraic understanding of the Coriolis force.

If you look up the equation for the Coriolis force, you'll see it stated as

where Ω is the angular velocity of the rotating frame (for Earth, 2π/day), and v is the velocity of an object in the rotating frame. You may notice, there's no mention of radius here, which is why I was confused by the articles I was reading.

I decided to follow the default route for Physics: Simplify until things make sense! Let's imagine a hurricane directly over the North Pole. A key feature of hurricanes is the eye, which is a region of low pressure at the center. Low pressure in the middle means air will tend to flow from the outside in. As that air accelerates though, it will have a velocity perpendicular to the angular velocity, which is pointing straight up in this case. That will cause the Coriolis force above to push the air in a counter-clockwise direction, exactly what we're expecting.

I tried to put together a full simulation of the pressure difference driving the air inward, but then being balanced by the Coriolis force spinning it in a circle. Unfortunately, I couldn't come up with a model of the pressure that didn't vastly overpower the Coriolis force, so I ended up simplifying things a bit more: We assume the pressure difference causes a constant force inward, and then see how that changes under the effect of the Earth's rotation vector, projected into the local plane of Florida (27.7° N latitude):

For this simulation, I used a diameter of 300 miles and a Category 3 windspeed of 120 mph, but again, I had to fudge a bit to get things to work.

As for the second part of the question, centrifugal force doesn't really come into things here. For most places on the Earth, centrifugal force points upward, so its only effect on the hurricane would be a vertical circulation of the air. That may have an effect in reality, but I'm only considering a 2D model here, so it doesn't really apply.

I always have a hard time picturing these 3D systems, with interacting vectors and different reference frames, but I hope I've given a reasonable explanation for how these types of weather events form. I'm betting there's a way to connect my understanding of Coriolis forces to the one commonly given, but I can't puzzle it out. Thanks for another great question, Papou!

Stochastic & Fantastic

As I've mentioned before, I keep a list of potential topics that I choose from now and then, and this week I thought I'd look back at an article that caught my interest 2 years ago. Scientific American had a story about a beetle that looked for recently-burned forests using a process called stochastic resonance. The beetles use this process to sense heat from great distances, when normally those heat signals would fall below the background levels. Paradoxically, they do this by adding more noise to the signal. I was curious if I could model this type of effect, to get a better feel for how it works.

In its simplest form, we have 3 parameters for this system: The signal strength, the amount of noise added to that, and the threshold for detection. The principle is that even if the signal is smaller than the noise, we still have signal + noise > noise. That means if we can pick our threshold so that noise < threshold < noise + signal, we'll be able to pick up the signal.

Following an example used in the Wikipedia article above, I decided to use a black & white image as the target signal. I settled on one of the more iconic photos of a certain physicist. Below, you'll find the 3 controls I described. Try turning down the overall signal, then adjust the noise and threshold to pick out different features.

The Error of Slitherin'

[I'm not placing any judgment on snakes' movement technique; I just couldn't resist the Harry Potter pun!]

Along with her obvious chihuahua roots, we suspect Lorna has some terrier in her, due to her dogged (heh) attempts to catch small animals, including (to my mother-in-law's horror) snakes!

During a walk this past week, I saw her lunge forward and I instinctively yanked back on the leash to see this fellow slithering away. I was hypnotized by the rhythmic motion, and was immediately curious how it worked.

Searching a bit online, I found a paper called The mechanics of slithering locomotion, which seemed like exactly what I wanted to know. The idea the paper puts forward is that the friction between the snake and the ground is different depending on which way it slides: There's less grip along the length of the snake than across it. You can see the difference in the pattern of scales:

Figure 1 from the paper

The paper goes into a lot of detail about making the snakes move at different angles and, of course drugging them for pictures, but I was curious if I could make a simple model based solely on the idea of direction-dependent friction.

Suppose the snake moves forward at a constant velocity, while moving sinusoidally in the transverse direction. We can write this as a parametric equation:

where v_x is the forward velocity, and A and ω are the amplitude and frequency of the side-to-side motion. Differentiating twice will give us the acceleration needed to maintain this motion. Of course, since the x-velocity is constant, the acceleration is zero, so turning to y,

That's in terms of the direction lateral to the snake's overall motion, but that's not what we're interested in. We want the acceleration in terms of the snake's body direction. The direction of the snake can be written as

We can plug in the derivative, normalize the vector, then use the equations

to get the components of acceleration parallel and normal to the snake. That gets a bit messy though, so I'll skip to the nifty animation:

As you can see, the forces perpendicular to the body (red) are much larger than the ones parallel (blue), requiring more friction as the paper found.

A Bolt of Cloth

The past couple weeks here have been non-stop drizzling rain – not the nicest farewell I could have – but it reminded me of a post from another of my favorite blogs, Futility Closet.

Wikipedia

Shortly after Benjamin Franklin created the first lightning rod, the idea caught on in Europe as a fashion accessory. There were umbrellas fitted with lightning rods (above), as well as hats, which trailed a wire for grounding. The information on these is a bit sparse, in particular whether they had ever been tested. This concerned me, since I saw some potential problems with the design, which I thought I'd explore today.

First, a quick explanation of how lightning rods work: During thunderstorms, charge collects in clouds. If enough charge builds up, it can overcome the resistance in the air, and create a channel down to the ground, where it discharges. This is lightning, which can carry lots of charge at high speed. Electricity takes the path of least resistance, and since humans and animals carry a lot of salty water, that makes us appealing routes to the ground. Tall buildings can also make good conductors, but since lightning carries so much energy, it can start fires. To protect ourselves, and our homes, we can make even better channels by topping buildings with a metal rod that connects directly to the Earth through a wire. Based on this, the lightning rod apparel doesn't seem unreasonable, but let's look at some issues.

Ground Current
For real lightning rods, the grounding wire is buried several feet deep to better distribute the charge, but that wouldn't be possible with a rod you carry with you. Instead, the wire just drags behind you, but that's no different from lightning striking the ground near you. Lightning carries a lot of charge, and it takes some space to dissipate, which can be just as dangerous as the initial strike. The National Weather Service webpage illustrates this with a charmingly-90s, yet still horrifying, animated GIF:

According to the Washington Post, ground current can be dangerous as far as 60 feet from the initial strike, so you'd need an awfully long tail on your umbrella/hat, not to mention the danger to anyone else who happens to be near the contact point.

Melting Wire
Since these are fashion accessories we're talking about, the Wikipedia article above mentions that the grounding wire was silver, but that could get expensive. One site I found lists the gauge for a grounding wire as 2 AWG, or about a quarter inch. There's also the problem that silver has a lower melting point than copper, 961.78 °C. That made me curious whether you'd be trading electrocution for being sprayed with molten silver.

The energy absorbed by the wire will be

where I is the current, 𝜌 is silver's resistivity, l is the length of the wire, A its area, and t is the duration of the strike. Using those values, along with a normal (rather than rope-sized) silver chain, and a height of 1.8 meters, I come up with 195 Joules, which is nowhere near enough to melt even a thin chain.

Magnetic Field
So at this point, you're still dead from the ground current, but your relatives will be able to salvage your silver chain. What about your smartphone? When current flows through a wire, it produces a magnetic field, according to

I couldn't find info for smartphones, but according to this site, credit cards could be damaged at a distance of 63 centimeters, and pacemakers at 25 meters! I'm not sure whether the short duration of the bolt would change these calculations, but it still doesn't seem like you or your electronics would be safe in a thunderstorm, even if you are wearing the height of 18th century fashion.

Big thanks to Futility Closet for pointing out this fleeting trend! I'm sure we would never use new technology in such a frivolous way, right?

A Tense Moment

A few days ago, I was sitting on the balcony at my parents' condo, and I noticed a water droplet on the leaf of their banana tree.

 

Seeing it got me thinking about surface tension, the force that gives it the characteristic shape that small drops have.

A simple way to think about surface tension is this: each molecule of water has a certain amount of attractive force between it and its neighbors.  However, at the surface, there are no molecules on one side, so the force associated with the other molecules is stronger.  Here's a diagram (from Wikipedia):

When a droplet like this sits on a solid surface, it will be spread out slightly by the force of gravity.  The height is given by

where ϒ is the surface tension between air and water, θ is the angle the water's surface makes with the leaf, and ρ is the density of water.  Plugging in the values we have, h = 4.1 mm.  Unfortunately, my photo doesn't include any scale, so I can't check how close this is, but it sounds reasonable.

I'll be leaving for Michigan in a few days to start grad school, so there will be a pause in posting while I move in.

Rain, Rain, Go Away

I've been trying to get this post done for the past couple days, but I've been feeling some of the fatigue I was warned about with the radiation, so I was a bit delayed.

It was another rainy trip in and out of Boston Thursday.  Steve's car has the interesting feature of wipers that automatically adjust their speed, using a sensor along the top of the windshield.  Watching them speed and slow with the rain got me thinking: the faster you drive, the more rain you'll hit, but the extra speed also drives rain up the windshield and into the sensor.  Do the two balance each other out, or will the wipers end up going too fast or too slow?

The most difficult part of this will be figuring out how fast the rain slides up the windshield, so we'll handle that first.  Once the rain hits the windshield, it's going the same velocity as the car, and it's the oncoming wind that will push it up.  The force of the wind drag is given by

where ρ is the density of air, v is the velocity of the water drop relative to the wind (basically the car's velocity), C is the drag coefficient, and A is the cross-sectional area of the drop.  To simplify things, we'll assume gravity is much weaker than this and take it to be the only force on the drop.  Then the distance it moves up the windshield after a time t is

where m is the mass of the drop.  If the drops are uniformly spread over the windshield, then on average they'll need to travel up half of it to get to the sensor.  This gives a rate of

where d is the length of the windshield.

Suppose the number of drops that have entered the sensor after a time t is n(t).  Then the rate of drops is

where rr is the rate of rainfall directly into the sensor.  The density of rain in the air (drops per volume) is

where vr is the velocity of the falling rain and As is the area of the sensor.  Using this, we can find the rate drops fall on the windshield

where θ is the tilt of the windshield.

Comparing to the rate the drops are entering the sensor, we can see that both are linear in v with a constant offset, meaning that for sufficiently high velocities, the relationship should work out evenly.  Clearly those Volvo engineers knew what they were doing...

Here Comes the Sun

While I've been home, I've been looking at Steve's weather station.  I hadn't noticed before, but in addition to temperature, humidity, and all the standard weather statistics, it also measures solar radiation and UV index.  Here are the plots of those two for the past 24 hours:

Today's been pretty cloudy, so things aren't that exciting, but there was a nice peak at 2:00 yesterday.  UV Index is a sort of strange parameter.  It's designed to be a simple indication of how damaging the sunlight can be to your skin.  Originally, it was meant to be on a scale of 0-10, with 5 and up indicating a risk of damage without sunscreen.  However, with the depletion of the ozone layer, the index can now rise above 10 in some places.

Looking at these plots together, I started wondering how much of the total solar radiation was UV light.  Unfortunately, the UV index is calculated by weighting the UV radiation with a function called the McKinlay-Diffey Erythema action spectrum.  The function varies according to how dangerous specific wavelengths are to your skin, but it never goes above 1, so we can at least get a minimum measure of the UV radiation.

At 2:00 yesterday, the UV index was about 4.25.  To convert this into radiation, we divide by 40, giving 106 milliwatts/meter^2.  The total solar radiation at that time was about 700 watts/meter^2, so the UV light made up a minimum of 0.01% of the radiation reaching Earth.  Not very much, but it goes a long way.

Wag the Dog, Part 1

I'm at home in Ashfield for the week, which means I get to spend time with our two dogs, Ida, a yellow lab, and Darcy, a Boston terrier.  Both dogs have an interesting habit of wagging their tails so violently that their whole body begins to wag too.  I put together a little illustrative animation:

The first thing that came to mind when I saw this was coupled oscillation, when two oscillators are connected, and the movement of one causes the other to begin moving as well.

When dealing with coupled oscillators, it's often useful to find their normal modes.  First though, we'll need to come up with some equations that govern this motion.  I'm thinking the best model is a sort of angular spring – the more a joint bends, the harder it tries to return to straight.  In this case, the equation for the joints would be

where τ is the torque, θ the angle the joint is bent, and k the spring constant.  We can turn the torque into a more useful measure of the joints' movement by using the moment of inertia of a rod, I.

where α is the angular acceleration, m the mass, and l the length of the segment of body.  In order to use the standard methods for coupled oscillators, we'll need to put this in Cartesian (x and y) coordinates.  Since the upper joint is fixed, we'll take as our points of interest the lower joint and the tip of the tail.  If we know where these two points are, we can find the positions of everything else.  For the lower joint, we have

and for the tip of the tail

so solving for the θs,

We also need the second derivatives of each of these. Starting with the first derivatives,

Then the second derivatives are

Whew, things are looking pretty ugly.  I'm going to stop here for now and pick this up again tomorrow.  Sorry to leave you hanging...