(Credit goes to xkcd for the title.)
On the way to Swarthmore last week, Steve's coat and tie were hanging above the car door across from me. As we went around curves, I watched the tie swing back and forth, and it made me start thinking about how a pendulum would behave in a turning car. Generally, physical laws only apply to inertial frames (that is, perspectives that are not accelerating), so we can't simply measure things in the car; we have to transform those measurements into ones made from a fixed point.
Starting inside the car, let's call the angle of the pendulum above vertical θ, and the length of the pendulum's string r:
In Lagrangian mechanics, the main things we care about are the particle's potential and kinetic energy. In this case, the potential energy is easy, since there's just gravity to worry about:
where m is the mass of the particle, and g is the acceleration due to gravity. The kinetic energy is a little more complicated, since we need to think about the car's motion. In the car's frame, the pendulum's position is
where y is the vertical direction and x the horizontal. We can transform this to a fixed frame velocity using
where ω is the angular velocity of the car, and the f and r subscripts denote the fixed and rotating frames respectively. Plugging in a, we have
where R is the radial direction in the fixed frame, and φ is the angle between x and ω. The kinetic energy then is
The Lagrangian is given by
so plugging in our values gives
The Euler-Lagrange equations for our variables are
so plugging in L gives
We can solve the second equation for θdot and plug it into the first one. Then solving for θdotdot gives
I don't think there's a good way to solve this exactly, but we can find a numerical solution for specific cases. First, we can look at the simplest situation where φ = φdot = 0.
Pretty standard pendulum motion, but now let's look at something a little more complicated. Suppose
Then we get motion that looks like this
I'm not sure what exactly the qualifications are for chaotic motion, but this may fit. In any case, I think it's pretty cool looking.







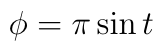


Would you explain what phi and phi-dot represent?
ReplyDelete