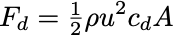Pulsar-Teacher Association

On Thursday, the NANOGrav project, along with international partners, made the announcement that they had detected a stochastic gravitational-wave background! This week, I thought I'd talk a bit about the news, and how the discovery was made.

First though, we should talk about what a stochastic gravitational-wave background is. Gravitational waves are produced whenever large amounts of mass move around in an asymmetric way. In the case of (still undetected) continuous waves, a bump on the neutron star, or for CBCs a pair of black holes or neutron stars. In the case of stochastic waves, we're talking about galaxies colliding, which is a much slower process. Since the movement is slower, that means the frequency is lower, on the order of nanohertz, or about 1/(32 years). That range of frequencies is far below what LIGO, or even LISA can detect:

Wikipedia

The orange region on the left is the background signals we're talking about, and the type of detectors used are called Pulsar Timing Arrays (PTAs). Pulsars are rapidly-spinning neutron stars, which produce pulses of radio-frequency signals at extremely regular intervals. They were initially referred to (jokingly) as LGMs, or "little green men", since it seemed like regular radio bursts would be a hallmark of an intelligent species.

The strength of a gravitational wave depends in part on the size of the masses that are moving. Since this background signal is due to entire galaxies moving, the gravitational waves are a million times stronger than those detected by LIGO! You might wonder then, why they were not detected before the CBCs that LIGO found. While I was thinking about this myself, an analogy occurred to me: Shifts in the Earth's tectonic plates are responsible for both earthquakes and continental drift. Even though the drift is on a significantly higher scale than the earthquakes, it's much harder to detect, due to the long periods (low frequency) involved, while earthquakes are picked up every day.

Since the first detection by Jocelyn Bell in 1968, many more pulsars have been found. The regular signals from these pulsars can be thought of as distant clocks ticking, from which the idea of pulsar timing arrays was conceived. A passing gravitational wave will cause a change in the signal's arrival time on Earth, but that change will depend on the direction of the pulsar, and the direction and polarization of the gravitational wave.

An isotropic signal means it should be the same in all directions. In 1983, Hellings and Downs suggested a method to detect such a signal: If two pulsars are affected by the same gravitational wave background, then the measurement of those pulse deviations on Earth should depend on the strength of that background, the noise in our measurements, and the orientation of the pulsar relative to Earth. By averaging the correlation between two pulsars over a long period, we can reduce the noise (which should be uncorrelated) and increase the background signal. Hellings and Downs derived a specific curve that that correlation should follow, according to the angle between the pairs of pulsars. After 15 years of collecting data from 67 pulsars, the collaboration presented this comparison to the expected curve:

Figure 1c

The points clearly deviate from the straight line that would result from no stochastic background signal, and instead follow the predicted curve, indicating a background signal is present. It's exciting to have another part of the gravitational wave spectrum filled in, and I look forward to more results from PTA groups!

Moonshotgun

I got another lunar question from Papou this week: If the same gun was fired on the Earth and Moon, proportionally, how much further would the bullet travel and would it have a greater velocity?

As I thought about this, there were a couple different effects that could make the bullet go further, so let's see how much each one contributes:

Drag

The most obvious difference between the Moon and Earth is the lack of atmosphere. That will come into a couple of these points, but this is the one most people might think of. When a bullet travels through the air, it needs to push the molecules out of the way. According to Newton, the air will push back on the bullet, creating a drag force:

where ρ is the air density, u is the speed of the bullet, A is the cross-sectional area of the bullet, and cd is the drag coefficient. The drag coefficient depends on the shape of the object, since some shapes are more aerodynamic than others. However, for bullets and other projectiles, people instead use the ballistic coefficient, defined as

where m is the mass of the bullet. We can combine these to write

where ad is the drag acceleration. The bullet is slowed down by this drag, meaning it won't get as far before hitting the ground. We can find the ballistic coefficient with tools like this one.

Gravity

Another difference that immediately comes to mind is the difference in gravity: The Moon has about 1/6 the gravity of Earth, which will make the bullet fall more slowly. The bullet's range is limited by how long it takes to hit the ground, so the Moon will allow the bullet to travel further.

Expansion of Gas

Bullets are propelled down the barrel by expanding gas from the gunpowder. Similar to the drag force above, on Earth air will get in the way. In this case though, rather than drag I think a better model is an opposing pressure on the other side of the bullet. If we assume the bullet has constant acceleration a down the length of the barrel L, then the muzzle velocity is 

On Earth, the acceleration will be given by

where P is the pressure from the gunpowder, and P0 is the ambient pressure. Putting everything together, we can get an equation for the muzzle velocity in vacuum based on the one from air:

Plugging in some typical values shows that the speed increase is pretty negligible.

Curvature of Body

Since the Earth and Moon are both (approximately) spherical, as the bullet travels, the ground will begin to slope away, increasing the time it takes for the bullet to hit the ground. When I first started thinking about this question, one thing that came to mind was Newton's Cannonball:

Wikipedia

As the muzzle velocity increases, the projectile has further to fall, until it reaches orbital velocity and continues falling without hitting the body. For short distances, we can approximate this as 

Putting It All Together

I put together some code to run a simulation of the bullet's flight on Earth and on the Moon, but I ran into some problems with the drag calculation using the ballistic coefficient. I ended up approximating the drag using the drag coefficient for a hemisphere. For the bullet/rifle parameters, I used the numbers from Wikipedia's .22 rifle page, although I also tried cranking up the speed to see the differences. By far, the greatest effect on the range is the decrease in gravity, but drag has some influence, particularly for the higher speed. The curvature has no discernible impact.

In case you're wondering whether a gun would even work on the Moon, Mythbusters tested a pistol in a vacuum chamber, and found that the gunpowder does contain all the necessary chemicals to ignite. In fact, during the Space Race, Russian cosmonauts carried the TP-82 Survival Pistol, reportedly to fend off wildlife in case of crashes in the Siberian wilderness, but you can imagine it was advertised in case American astronauts got any ideas. Thanks for a great question, Papou!

GRACE is Beauty in Motion

This week, I heard two talks on the Gravity Recovery and Climate Experiment (GRACE), an experiment being developed by some of my colleagues here in Florida. The goal of the experiment is to measure variations in the mass distribution of the Earth, using a pair of orbiting satellites:

JPL

As the satellites orbit, they pass over regions of greater and smaller mass, causing them to speed up or slow down. These variations will affect the leading spacecraft first, causing the separation between them to change. We can measure these changes with a laser interferometer, just like the ones used by LIGO and LISA. This results in a detailed map of how mass is distributed over the planet:

JPL

The heaviest points (in red) tend to be in mountain ranges, like the Alps and Andes.

You might be wondering (as I did) how this relates to climate. The key is that water is dense stuff, so when it moves around, it can significantly change the pull of gravity. As snow and ice melt, the water will flow to different places. The researchers have made their data available online, so I tried putting together some code to make summary plots.

The data I linked to above records the liquid water equivalent thickness, which is the depth of water over an area that would result in the measured mass per area. It covers 2002 to 2020, giving a planet-wide measurement every month. I plotted the data on a Mollweide projection and animated it in time:

I wasn't able to make it as clean as some of the diagrams the presenters showed, but you can see some seasonal variations, particularly in the Amazon region, and you can see things get significantly redder as time goes on. Looking at a single point in the middle of the North Atlantic shows an alarming trend:

As the glaciers and ice caps melt, that water flows into the oceans, raising the levels. On top of that, warm water expands, so any kind of heat added to the oceans will increase the depth. I hope we can use tools like GRACE to learn how best to reverse trends like this, and how to emphasize how necessary it is!

Itty Bitty Bang

 Another question this week from Papou: Since a Black Hole can continuously acquire mass (except those cases wherein it loses matter per S. Hawking), does it follow that those Black Hole’s Event Horizon is also continuously getting larger. If that were not the case and the Event Horizon continuously reduced its boundary, does it not follow that Black Hole would become a point mass followed by a Big Bang. If that were the case, then it would be irrational that there was only one Big Bang and we are the product of that singular Big Bang. It is more likely, then, that there may have been other Big Bangs and there are other Universes out in Space. Is there anywhere in space where the Red Shift is not consistent with our Big Bang; which would then imply that there may have been multiple Big Bangs.

I think you get my drift ..... basically I am saying:   “Can a Black Hole become a Big Bang? What is the latest Red Shift evidence?

There are a couple different issues at play here, so let's address them one by one. First off, the event horizon of a black hole: A black hole is a region of space where matter has become so dense, light cannot escape its gravitational pull. The size of that space, called the Schwartzschild radius, is proportional to the amount of mass inside it:

where G is the gravitational constant, M is the mass, and c is the speed of light. You can actually find this yourself by looking for when the escape velocity is equal to c. This radius is sometimes called the event horizon, since in Special Relativity, events are described as points in space and time that are observed through light. If light cannot escape the black hole, we cannot observe events within it.

That brings us to the next part of the question: What happens to a black hole over time? As the equation above states, the event horizon radius is directly proportional to the mass within it, so if it loses mass due to Hawking radiation, or gains mass due to objects falling it, the radius can shrink or grow, but for fixed mass, the event horizon should stay fixed. For small black holes, Hawking radiation can eventually reduce the mass to zero, which is believed to result in the black hole evaporating. As the black hole shrinks, it will cross between the theories of General Relativity, and Quantum Mechanics. In their current forms, these theories are incompatible, but it's believed the evaporating black hole would release a burst of gamma rays as it vanished.

Still, there is a connection between event horizons and big bangs: In 2013, a group of scientists proposed that our universe could exist as the event horizon of a black hole in 4 spacial dimensions. In our 3 spatial dimensions, an event horizon is the surface of a sphere, which is 2D. A 4 dimensional black hole though would result in a 3D event horizon. Of course, that implies the possibility of a 2D universe on the event horizons of our universe.

Finally, the connection to red shift: The universe is expanding at every point, which means every point is moving away from every other point. I often find it helpful to imagine a big rubber sheet being stretched outward; any two points drawn on the sheet will get farther apart. As light moves through the universe, its wavelength gets stretched too, making it "redder", i.e. lower frequency. If you point a radio telescope at an empty part of the sky, as Arno Penzias and Robert Wilson did in 1965, you'll find a constant signal in the microwave band of light, called the Cosmic Microwave Background (CMB). This light is distributed in the blackbody spectrum, the range of photons emitted by objects of a given temperature. That temperature is from 380,000 years after the Big Bang, when things had cooled enough for protons and electrons to combine into hydrogen, about 3000 Kelvin. Over the billions of years that light has travelled, it's been red shifted down to around 2.725 Kelvin, in the microwave range.

If you look at a picture of the CMB, you may notice that it's not entirely uniform:

NASA

These anisotropies are mainly due to gravity pulling particles into clumps, which cool differently. Some have suggested the CMB also contains evidence of "bruises" from collisions between our universe and others existing in a larger multiverse. However, no such collisions have been detected so far.

Thanks for another great question, Papou!

Not So Oblious

Marika and I have been getting ready to head down to Florida this coming week, and while paying a farewell visit to her grandparents, Papou posed another of his fascinating questions: Given the Earth is an oblate spheroid (flattened at the poles and bulging in the middle), what direction does gravity point relative to the surface?

If we take a cross-section of the Earth through the poles, we get an ellipse, which is given by the equation

where a and b give the half-width and half-height of the ellipse respectively. We want to try varying these two values to see what happens to the gravity. If we assume a constant density, we can keep the total mass constant by fixing the area of the ellipse:

We can also consider the eccentricity of the ellipse, given by

Using these, we can rewrite a and b as

Newton's Law of Gravity says the force between two masses is

where m1 and m2 are the two masses, r is the distance between them, and G is Newton's constant. For our elliptical planet, we can add up little bits of mass throughout the volume to make a complicated integral:

where ρ is the mass density and A is the space covered by the ellipse. Initially, I thought I could avoid evaluating this nasty object by using Gauss's Law, which would suggest that the pull was always toward the center, but the ellipse doesn't offer the necessary symmetry. I decided to prove this to myself by throwing the integral at Python to solve for me:

The red line goes to the origin, and the black arrow points in the direction of gravity, as found from the integral above. You can see that for large eccentricities, the arrow begins to diverge. We can plot the angular difference:

We get up to around 12° difference, which suggests that an assumption of radial gravity won't cut it. Unfortunately, the numerical integration is both slow, and has inaccuracies for certain points. That leads to some uninformative plots:

Here, theta is the angle from the x-axis, and the horizontal gravity is in arbitrary units. The integrator has problems when it gets to the edges of the ellipse, which leads to some of the force arrows going nuts. If we disregard the deviation discussed above, and assume the gravity really does point toward the center, we can get a much smoother graph, which roughly matches the true solution:

As a check on this, it's often useful in Physics to consider the most extreme case (e.g. zero or infinite mass, length, energy). For this system, we could imagine a planet that was flattened into a disk. The mass ends up concentrated in the center, tapering off toward the edges. If you stand in the center, gravity pulls straight down, but moving away, it would begin to pull back toward the center. If you were standing on the edge of the disk, the center would be straight down, so there's no horizontal force. This leads to the 4 zeros on the plot above: the centers of the top and bottom, and the right and left edges. Thanks for another great question, Papou!

Filling in the Holes

Following up on some previous posts about gravitational wave detections, this week I have some questions from Papou:

How many current black hole collisions are we aware?
Last year, the LIGO/Virgo Collaboration released the first Gravitational-Wave Transient Catalog, covering all the detections from the first and second observing runs. That includes 10 binary black hole (BBH) events, and 1 binary neutron star (BNS) merger. The third observing run is split in two pieces. Results from the first half, O3a, are available on GraceDb, and include 37 BBHs, 6 BNSs, 5 neutron star black hole (NSBH) mergers, and 4 events that fall in the "mass gap".

The mass gap represents a range of masses where we have never seen a black hole or neutron star. This image shows a summary of the compact objects observed by LIGO and electromagnetic astronomers as of the end of O2:

via Northwestern

The empty space between 2 and 5 solar masses is the mass gap. It is unknown what kind of bodies were involved in those mass gap collisions.

What happens to "Matter and Antimatter" when two black holes collide?
Black holes are made of matter. When matter and antimatter combine they make energy, but as with most physical processes, this is reversible: energy can create matter/antimatter pairs. Since the universe contains residual heat energy from the Big Bang, these pairs are constantly forming and annihilating back into energy in space. If one of these pairs forms near a black hole though, the antiparticle can fall into it, while the matter particle escapes. This process is called Hawking radiation, and can lead to a black hole losing mass.

Are photons escaping due to the collision energy?
In the case of black holes, no. Light can't escape a black hole's event horizon, and when two collide, their horizons merge. Neutron star collisions, however, can release photons in the form of a gamma-ray burst (GRB). In an earlier post, I mentioned LIGO's detection of GW170817, which showed a correlation between a binary neutron star merger, and a GRB.

Are the combining gravities simply arithmetic additions or does the total gravity grow in multiples?
Neither! Mass and energy are connected through E = mc^2, so when energy is released in the form of gravitational waves, part of that comes from the masses of the black holes. Despite the extreme sensitivity needed to detect gravitational waves, they carry an enormous amount of energy. The first detection, GW150914, lost about 3 suns worth of mass-energy. I tried to find a way to put that number in perspective, like "X billion nuclear bombs", but it's so huge that it dwarfs even a measure like that. Spacetime is exceptionally stiff stuff, and wrinkling it even a little needs an amount of energy that we don't normally encounter.

Thanks for more great questions, Papou!

A Singular Family

This week, I got some great questions from my nephew Ezra, along with his parents Nate and Carrie. I gave them some quick answers off the top of my head, but I thought they deserved a more in-depth treatment as well.

Ezra: What does a gravity wave feel like [to a person]?
As a reminder, gravitational waves warp space as they pass. If a wave passed through the center of a hula-hoop, it might look like this:

Each image is a point in time. Adapted from my thesis.

Gravitational waves are incredibly weak, which is why we need 2.5 miles of detector to pick them up. They’re a squeezing and stretching of space, so if you could feel them, they’d be a combination of a hug (awww) and a medieval rack (ahhh!). Some of the early detectors were big pieces of tuned metal that scientists hoped would ring like a xylophone if the correct frequency passed by. Those were never sensitive enough though.

Nate: But aren't they weak because they're distant? What if you were closer to a pair of black holes approaching collision? Could you be close enough to feel the waves but far enough to not be inside?

Good point! We can take the first LIGO detection, GW150914, as an example. According to that paper, the distance was about 410 megaparsecs, and the peak strain was 10^-21. Strain is the fraction by which the wave changes distances, so a meter stick would be stretched and squeezed by 1/1000000000000000000000 meter! That's pretty tiny, but strain drops off as 1/distance, so we can get a bigger effect closer to the collision. We probably don't want to be inside the event horizon of the final black hole, which has a radius of

Plugging in the 62 solar masses from the paper, we get 183 km. Supposing a 6 ft person observed the collision from 200 km away then, their height would change by a little over 4.5 inches!

Carrie: Is a black hole a hole in space-time or a depression?

It's both! -ish. This is a difficult question to answer, since the whole point of a black hole is that we don't know what's going on inside it. The trouble is that when a star collapses into a black hole, it creates a singularity – a point of infinite density. That creates a lot of problems for General Relativity, since things falling into the singularity could wind up going faster than light, and other bad things that happen when you have an infinite quantity. Instead, we put an event horizon around the singularity at the point where light can no longer escape from it, which is usually where bad stuff starts. Wikipedia has some nice representations of a singularity with and without an event horizon (bad stuff not included):

Black hole, via Wikimedia Commons

Naked singularity, via Wikimedia Commons

Thanks for some great questions!

Intelligent Falling

[Title refers to the equally credible explanation for gravity.]

I'm in the middle of reading Seveneves, by Neal Stephenson, which involves humanity fleeing the surface of Earth to survive in orbit. All the discussion of orbital mechanics reminded me of a program I loved playing with when I was growing up called Gravitation, Ltd. It let you set up bodies of different masses in space, and let them move according to each other's gravity. What I particularly liked seeing was the different patterns the orbits would make. Since that application is more than 20 years old at this point, I was curious if I could set up another HTML5 widget to play with.

For any pair of objects, Newton's Law gives the acceleration of one object created by the other:

where G is Newton's constant, m is the mass of the attracting object, and r is the vector from the accelerating object to the attracting one. This is a second-order differential equation for the position of the body: The equation gives an acceleration, which is the change in velocity, which is the change in position. At every step of time in our simulation, we need to find the acceleration, and from that get the velocity and position. The natural way to do that, integrating up from acceleration, would be

where the subscript indicates the step number. This is called Forward Euler Integration. For certain systems though, this method can be unstable, producing results that diverge to infinity. A more robust technique is Backward Euler Integration, which does the calculation in the opposite order:

Both are implemented below, but I haven't noticed much difference for the cases I've tried. Play around a bit, and be sure to post interesting settings in the comments!

Canvas not supported; please update your browser.

Initial Position

Initial Velocity

Star Mass

Method

Forward Backward

Tennesseein' is Tennebelievin'

[Title thanks to The Simpsons]

My brother-in-law Dave Willett sent me an op-ed from the Tennessean titled "Primary cause of global warming is force of gravity". Normally I hesitate to comment on science outside my expertise, but by attributing climate change to gravity, the author has brought this into my wheelhouse.

What's dangerous about this piece is that it mixes accurate information with unsupported conclusions. I thought the best way to tackle it would be a running commentary.

Climate change throughout planet earth is occurring and is observable, measurable, provable and, most importantly, unavoidable. Through numerous empirical methods the inexorable warming trend is being monitored and documented by researchers throughout the world. Thus mankind's influence on weather patterns and global warming is minuscule compared to the colossal heat-producing forces within the earth itself.

The main thing that bugs me about this passage is "thus". It suggests that the first part is in any way connected to the second, when in fact mankind's influence is painfully clear:

Wikipedia

Each line represents a different temperature-recording technique. Notice the massive uptick during the 19th and 20th centuries, strongly correlated with the advent of industrialization. This plot alone contradicts the author's thesis: Warming from the Earth's mantle would be a constant effect, with no connections to human history.

[...]
The earth itself is a heat-generating machine and is gradually warming, as is virtually every other planet, star and asteroid in our universe. The primary cause of this increase in global temperature is purely and simply the force of gravity. Due to the ubiquitous, ever-present force of gravity, our earth is gradually and inexorably shrinking. The force of gravity at the earth's surface is 9.80 m/sec/squared and increases greatly as it is measured closer and closer to the center of the earth. Gravitational pull increases the internal pressure in the earth itself and thus increases the internal temperature.

There's a lot wrong here, but one thing that's (almost) correct: The acceleration due to gravity is 9.8 meters/second^2 at the Earth's surface. Newton's Law of Gravity states

where a is the acceleration from gravity, G is Newton's constant, r is the distance to the center of mass, and M_enc is the total mass enclosed in that radius. If you plug in the radius and mass of the Earth as a whole, you will indeed get 9.8 m/s^2. However, as you descend into the Earth, not only will r get smaller, but so will M_enc. If the mass is equally distributed in a sphere, then the mass enclosed at a certain radius will be a ratio of the volumes:

where M_tot and R are the total mass and radius of the Earth, respectively. If we plug this into the equation above, we find as you descend into the Earth, the acceleration actually decreases:

This makes sense if you imagine being in the exact center of the Earth: Which way is gravity pulling you? The Earth is symmetric around you, so there can be no preferred direction, and the acceleration must be zero. It is true that the rest of the Earth is pushing in on you, creating pressure and heat, but that brings us to the next part.

The laws of thermodynamics teach us that heat is transferred by three methods: conduction, convection and radiation. Consider the colossal heat within a few thousand feet of the earth's surface and that this heat is transferred by all three phenomena, through conduction heat is transferred to the earth's surface through the tremendous dynamic circulation of the astronomical volume of molten metal and rock. Convection currents transfer heat to the earth's surface, and the radiation of the incredibly hot geological structures also raises the temperature of our environment.

Radiation of heat is an important point for climate change. Normally, heat created by the planet is radiated into space. The excess of CO2 and other greenhouse gasses, however, reflects this heat back to the surface. From here the author goes into effects of tectonic shifts, which I won't get into, because that's not my area of expertise! 

The author emphasizes the dangers of climate change, which is a great position to have, but without understanding the causes, it's impossible to arrive at a solution. As much as I mourn the decline in society's evaluation of science, worse is the misuse of science to arrive your own desired conclusion.