For some reason, my bus the past week has been especially full, forcing me to stand for most of my commute. I'm always surprised by how difficult it is to keep my balance going around curves, so I thought I'd try putting some hard numbers to the issue.
I've talked about the strange, non-inertial effects of being in a turning vehicle before, but this situation is much simpler. When the bus goes around a turn, it drags my feet along with a centripetal acceleration. Balance is all about keeping the total forces on you over your feet:
Here, ar is the centripetal acceleration of the bus, and g is the acceleration from gravity. Using geometry,
When something moves in a circle with radius r and velocity v, the centripetal acceleration is
Putting these together and solving for v gives
The turning radius for a standard city bus is about 21.5 feet, and the maximum angle a person can lean is around 15°. Putting these together gives a speed of just 9 mph! As a non-driver, I don't really have a feel for typical turning speeds, but the National Association of City Transportation Officials suggest a maximum of 15 mph, so our limit is well below this. Of course, when you're riding a bus you can lean into the curve, and hold on to the railings, neither of which we've accounted for here. Still, I feel a little justified in lurching around awkwardly during my commute.
Ok, doesn't quite scan, so I guess he's not destined for TV stardom, but one of his ideas is at the core of this week's post. Last week, I was talking to my parents over Facetime and Steve, ever the stickler for visual quality, complained that my lights appeared to be flickering:
Looking at it from my end though, the light appeared fine. I realized that the LED bulb must be flickering (by design) at a rate higher than my eyes can perceive, but my laptop camera is recording below the Nyquist rate, causing the flickers to appear.
Before getting into that, let's talk about how LED bulbs work. LEDs require direct current (DC), while house power is alternating current (AC), so the first thing we need to do is convert between these two. Alternating current is a sinusoid, oscillating between positive and negative of a certain value:
There's an electrical component called a diode that only allows current to flow in one direction. In fact, that's the D in LED, but right now we're just talking about the regular kind of diode, not the Light Emitting ones. By arranging a few of those in a clever way, we can switch the negative part of that curve to positive:
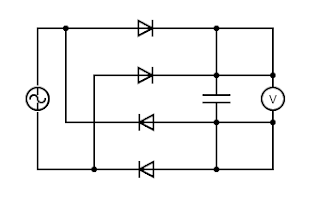
On the left is the AC source, and on the right is a voltmeter. The diodes in the middle only allow current to flow in the direction of the arrow. The voltmeter's output looks something like this:
This isn't ideal though, since the voltage is going all the way down to zero. We need a way to smooth out this curve. We can do that by adding a capacitor, which stores and releases charge as the voltage changes:
Now the voltage looks something like this:
Still not perfect, but it's the best we can do with something simple. Those little bumps mean the LEDs will be flickering a tiny bit, but it's at twice the rate of the original AC input. In France, this is 2x50 times per second (Hz).
The camera on my laptop captures video at about 30 frames per second. According to Nyquist, to accurately record a signal, we need to take data at twice the rate that the data changes, but that would be 200 Hz, far above what my camera is capable of. We can see why this is necessary by considering a point moving in a counter-clockwise circle:
The dot completes a cycle every 8 steps. The image on the left is sampled every step, while the one on the right is sampled every 7 steps. The slower sample rate causes the dot to appear to be moving backwards. You've probably seen a similar effect in videos which include old TVs or computers that used CRT screens. The screen appears to blink because the camera captures the screen at different points in its refresh.
That leaves us with the question of why the light doesn't blink according to our eyes. That's addressed by the flicker fusion threshold, which comes from the spectacularly-named field of psychophysics. Our eyes aren't able to perceive changes in intensity above a certain rate, instead averaging things out. For most people, it's around 80 Hz, so the LEDs easily surpass that, but the captured video is nowhere close.
My office is built into the side of a hill, and several times while waiting for my bus, I've seen bicyclists rocketing down at tremendous speed. I was imagining they would burn through their brakes quickly, and wondered if there were a better way to limit your speed on a hill. Switchbacks used by hikers came to mind – Instead of taking a direct route up a mountain, trails wind back and forth, which reduces the slope. I was curious if a similar method could be used to slow down.
If we ignore air/rolling resistance, we can use conservation of energy to relate the drop in height to the total velocity gained:
For a road of slope m, we can set up a differential equation relating this total velocity to the individual forward, sideways, and vertical velocities:
Suppose we want to maintain a constant forward velocity, and so any extra gets put into the side-to-side motion. Then we can get the total forward travel just by multiplying the velocity by t, and we can write the sideways speed as
The trouble with this strategy is that as you go downhill, your total velocity is increasing, but your forward velocity is constant. That means proportionally, you'll be traveling far faster sideways than the direction you're planning to go. I picked a 30% slope and 10 m/s forward speed to plug into the equation above:
After only about 10 seconds, 90% of your speed is perpendicular to the direction you want to go! Now that doesn't mean you'll never get to your destination – That speed is fixed, remember. Because we ignored resistive forces, your total velocity keeps increasing. I suppose it may be better to stick with the brakes – Not only does this method still have you going at uncomfortably high velocities, you'll also take a lot longer to get where you're going.
I missed posting last week because I was in Geneva visiting CERN! Marika was flying home via the city, and my brilliant mother-in-law suggested we take a tour of the facility. I thought I'd take this week to explain a bit about how the collider works.
The first CERN particle collider
CERN is the European Organization for Nuclear Research, but the umbrella of "nuclear research" extends farther than you may think. When researchers needed a way to share data between sites over the world, they developed a communication network between their computers that became the World Wide Web. We actually saw the very first web server, kept in a dimly lit room (its natural habitat), so I couldn't get a picture.
The main thing CERN is known for though is the Large Hadron Collider. I talked a bit about particle accelerators in my second-ever post on this blog, but that was just about getting particles up to a certain speed, not colliding them with other particles (aside from my brain).
The purpose of particle colliders is to create new particles by smashing together pairs of other particles. The key lies in what is probably the most famous equation in science:
This equation connects energy to mass, but energy comes in many forms. In this case, we give the initial particles kinetic energy by accelerating them. When they collide, that can be converted into mass energy to create higher mass particles.
The various particles in the Standard Model each have different masses, with the Higgs Boson being the heaviest. Heavier particles have more energy, which means we need faster initial particles to produce them. We can modify the equation above to include the velocity:
As the velocity, v, gets closer to the speed of light, c, the energy gets bigger and bigger. This is why you can never get up to light-speed: You'd need infinite energy. By accelerating lighter particles though, we can hope to create heavier ones.
While the Standard Model is now complete, there are other theories to go beyond it. The LHC is currently being upgraded to handle even higher energies in the hopes of confirming or refuting these theories. I loved seeing all the bits of science history they have there, and I encourage anyone passing through Geneva to go take a look!
