Spinning My Wheels

This week I changed the toilet paper in my bathroom, and it got me thinking about the rotational properties of a roll – When you try to spin something, you have to fight against rotational inertia, which depends both on mass, and how far from the center it's distributed.  That's why figure skaters speed up their spin when they pull their arms in:

What made me curious is that as the roll turns, the radius decreases, which lowers both the inertia and the torque that spins it.  Do these balance out?  I figured I'd try modelling what happens if you drop a roll while holding one end.

Since we're only interested in the roll rotating in the usual way, we can consider things in 2D:

We can find the rotational inertia by thinking of the roll as a disk with radius r(t), minus a smaller disk of radius r_i:

where ρ is the mass-density of the roll.  Now we can set up a bunch of other equations that we need.  By holding on to the end, we're applying a torque:

where α is the angular acceleration of the roll.  If we suppose each sheet has thickness T, we can relate the radius to the angle the roll has turned through:

Finally, we can integrate to connect the angle to the distance the roll has dropped:

Combining the torque and radius equations gives a differential equation:

This is fairly simple to solve by integration:

but I'm having trouble getting a plot.  I guess this is another week with complex equations leading to unsatisfying results.  Thanks for sticking through :)

MeteoRing

Shortly after I mentioned my girlfriend Marika, I'm delighted to announce we got engaged!  A few days later, we went shopping for my ring, which arrived earlier this week.  The metal used in the ring comes from a meteorite that hit the Earth during prehistoric times, and scattered over 8,000 square miles in the region of Africa that gives the meteorite its name: Gibeon, Namibia.

The unique design on the surface of the ring is called a Widmanstätten pattern, and is evidence of its extraterrestrial origins.  The pattern forms when a mixture of nickel and iron cool over a long period of time, on the order of 10 million years.  Such slow cooling isn't possible on Earth, where the rest of the planet can serve as a heat-sink.

The name "Widmanstätten" comes from Count Alois von Beckh Widmanstätten in 1808, but the first published study was actually from G. Thomson in 1804.  There's quite a story behind why he was not acknowledged (from Wikipedia):

Civil wars and political instability in southern Italy made it difficult for Thomson to maintain contact with his colleagues in England. This was demonstrated in his loss of important correspondence when its carrier was murdered. As a result, in 1804, his findings were only published in French in the Bibliothèque Britannique. At the beginning of 1806, Napoleon invaded the Kingdom of Naples and Thomson was forced to flee to Sicily and in November of that year, he died in Palermo at the age of 46.

It seems like a perfect choice for an astrophysicist, and a wonderful start to the next chapter of our relationship.  Thanks Marika!

Not Quite "Beam Me Up"

Last month, a group from Calgary announced they had broken the record for quantum teleportation over fiber-optics, so I thought I might talk a bit about the idea of quantum entanglement.

One of the main concepts behind quantum mechanics is that every particle has a set of states that can be measured.  It's possible for a particle to be in a mixture of several states, but once you measure a property, it "collapses" into a single state.  This idea is usually introduced with the property of spin, which you can think of as an arrow pointing out of the particle.  We can detect this spin with something called a Stern-Gerlach apparatus, which you can think of as a box with one input, and two outputs:

 

The two outputs tell you whether the spin is aligned with the angle of the box (+) or opposite the box (–).  If the particle goes in sideways, as shown above, then there is a 50% chance of it coming out each port.  However, when it comes out, it will have changed its spin to straight up or down, and all information on its previous sideways state will be lost.  In quantum mechanics, the initial sideways state is described as a superposition of the + and – states of the box: The particle is literally in both states at the same time.

Entanglement refers to two (or more) particles whose states depend on each other.  In the framework we've been discussing, we could imagine a device that puts out pairs of particles that have opposite spin.  Once we measure the spin of one, we immediately know what the spin of the other is.  This instant change of state for the unmeasured particle is called quantum teleportation.  If we put one of the particles in the box above, and it came out +, we would immediately know that the other particle was aligned opposite the box, no matter how far we had separated the two particles before making the measurement.

The idea of the new state being transmitted instantly over a great distance might worry you, since that would appear to be information traveling faster than light, which Einstein showed was impossible.  However, the state the two particles end up in is still random, even if they're guaranteed to be opposite each other.  The only way to observe this correlation is by comparing the spins conventionally at sub-light speeds.

Richard Feynman once said, "If you think you understand quantum mechanics, you don't understand quantum mechanics," but I hope I've given some insight into one of the frontiers of modern physics.  As always, questions are welcome!

Let Them Heat Cake

[Programming Note: I've noticed looking through older posts that the equations have picked up extra + signs, due to my impolite hotlinking.  I plan to go through and fix those when I have a chance, but until then, don't take them at face-value.]

Another great question from a reader, this time my own mother, Sally: I’m making a carrot cheesecake for Steve’s birthday. The cheesecake layer is supposed to go into an 9” springform pan but I only have 8”[...] I assumed I’d just make the cheesecake layer thicker, but how to determine baking time? The volume is the same but the height is 25% greater. Thicker tends to mean longer baking. But how do i determine that? What role does oven temp play? What role does moisture level of cheesecake play?

I've talked about heat transfer before, in this post about making granita, but I'd like to take a different approach this time, using the more general heat equation:

This says that the rate of temperature change at a point in the cake is proportional to the variation in temperature nearby, and the thermal diffusivity, α.  This quantity depends on the substance we're interested in, but I don't think it's been tabulated for cheesecake batter, so we'll assume it's about the same as water, 0.143 × 10⁻⁶ m²/s [this is the role the moisture level plays].

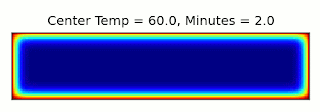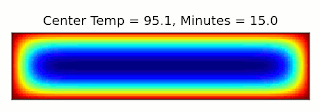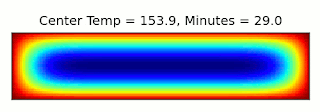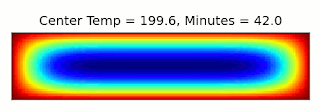
Technically, this is a 3-dimensional problem, but thanks to the cylindrical symmetry of the cake, we can just consider a 2d cross-section through the center.  We can assume the outer surface of the cake is fixed at the oven temperature, 325°F.  Then we can use a numerical solver to find the temperature throughout the cake over time.  As it happens, I wrote a solver for this equation a few years ago for a Computational Physics class.  After a few adjustments, it was ready to go: bake.py

First, we need to find the internal temperature that the cake reaches after the prescribed 45 minutes of baking.

The final temperature after 45 minutes is 206°F.  This is a little close to the boiling point of water, 212°F, where I expect things to get a bit off from the approximations I'm making, but we'll go with it.  Then we can start again with a narrower cake of the same volume, and find how long it takes to get to that temperature.

The final time is about 70 minutes, which isn't completely unreasonable, but I take no responsibility for any charred cakes this calculation results in.  Thanks for a great question, Sally!

[Edit: One first posting, I mistakenly used 8/9" as radii, rather than diameter.  It doesn't actually make a difference in the final results, since the thickness dominates.]

Precipitous Power

We've been getting a lot of rain here in Ann Arbor the last few days, and it reminded me of a question I've often wondered after being hit in the head by a particularly large drop: How much power could you generate from rainfall?

The kinetic energy of each drop is

where m is the mass and v is the velocity when it hits the ground.  Clearly we need some statistics about raindrop size; a quick search turned up this paper, from a collaboration between Brookhaven National Laboratory and a group of Chinese institutions.  The important info we need is in Fig. 5:

The y-axis, volume-mean diameter, refers to the diameter of a perfect sphere with the same volume/surface area ratio as the drop.  Coincidentally, this is also known as the Sauter mean diameter.  Unfortunately, the paper doesn't provide a fitting function for these curves, but we can take a guess, estimating values from pixels:

x	y
1.149825784	0.8509578544
3.066202091	0.9689655172
4.982578397	1.078544061
7.857142857	1.137547893
13.79790941	1.230268199
27.21254355	1.348275862
48.67595819	1.390421456

I chose the convective points for their larger range of rates.  Based on those, I asked R for a log fit and got this, with an R-squared of 0.992:

The relationship between mass and diameter is

where ρ is the density of water.  We still need to find v, but if we assume the drops hit terminal velocity for a sphere, we can use eqn 3 from this paper:

where g is the acceleration due to gravity, and I've substituted in the drag coefficient for a sphere.  Putting these together, the energy becomes

This is the energy of each drop, so we need to multiply by drops per time to get power.  The drops per time is related to the rain rate from above:

where A is the collection area.  Putting everything together, we have

If we plug in values, this comes to

At the highest rain rate from the paper, this comes to 0.081776 Watts per square meter, while solar cells can put out a couple hundred Watts per square meter, so maybe not the solution to our energy problems!

This one wound up being a bit dense, sorry.  I'll try to pick a more accessible topic next time!