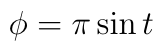You spin me right round, baby, right round, in a manner depriving me of an inertial reference frame. Baby.

(Credit goes to xkcd for the title.)

On the way to Swarthmore last week, Steve's coat and tie were hanging above the car door across from me.  As we went around curves, I watched the tie swing back and forth, and it made me start thinking about how a pendulum would behave in a turning car.  Generally, physical laws only apply to inertial frames (that is, perspectives that are not accelerating), so we can't simply measure things in the car; we have to transform those measurements into ones made from a fixed point.

Starting inside the car, let's call the angle of the pendulum above vertical θ, and the length of the pendulum's string r:

In Lagrangian mechanics, the main things we care about are the particle's potential and kinetic energy.  In this case, the potential energy is easy, since there's just gravity to worry about:

where m is the mass of the particle, and g is the acceleration due to gravity.  The kinetic energy is a little more complicated, since we need to think about the car's motion.  In the car's frame, the pendulum's position is

where y is the vertical direction and x the horizontal.  We can transform this to a fixed frame velocity using

where ω is the angular velocity of the car, and the f and r subscripts denote the fixed and rotating frames respectively.  Plugging in a, we have

where R is the radial direction in the fixed frame, and φ is the angle between x and ω.  The kinetic energy then is

The Lagrangian is given by

so plugging in our values gives

The Euler-Lagrange equations for our variables are

so plugging in L gives

We can solve the second equation for θdot and plug it into the first one.  Then solving for θdotdot gives

I don't think there's a good way to solve this exactly, but we can find a numerical solution for specific cases.  First, we can look at the simplest situation where φ = φdot = 0.

Pretty standard pendulum motion, but now let's look at something a little more complicated.  Suppose

Then we get motion that looks like this

I'm not sure what exactly the qualifications are for chaotic motion, but this may fit.  In any case, I think it's pretty cool looking.

Waxing Rhapsodic

I've been at Swarthmore enjoying Senior Week activities and my graduation yesterday morning.  One night last week, the dining hall served us an elegant, candlelit dinner.  I mention the candlelit part because looking at this

how could I avoid thinking about the physics of dripping candle wax?

As the wax melted, it would run down the column of solidified drips, until it reached the bottom.  It would sit there until it cooled and solidified, unless a second drop reached it first, in which case the combined weight would be too much, and they would both drip off.

To figure out how quickly the wax was cooling, we can use Newton's Law of Cooling.  Unfortunately, I couldn't find anything that explicitly gave the cooling rate for wax, but I did find some example data from a cooling candle.  Fitting the exponential form given by Newton's law to this gives

I'd estimate it took a little under a minute for each drop to solidify.  Supposing the wax solidifies at about 60°C, an initial temperature of 61°C would say that it remained molten for about 45 seconds.

We can figure out how much power the candle was putting out by looking at how much energy is required to raise the wax from room temperature to 61°C.  Using the equation

where ρ is the density of the drop, V its volume, and c the heat capacity of the wax, we find that it takes 0.08 Joules of energy to raise the temperature of a cubic millimeter of wax.  Since this involves melting the wax, we also need to take into account the latent heat of the wax.  This is the amount of energy required to induce the actual phase transition.  It's actually a pretty significant amount, and brings the total energy to 0.23 J.  If the candle is producing this much energy every 45 seconds, then its power output is about 5 milliwatts.  According to this page, candles put out something like 100 watts of power, so clearly not all of it is going toward melting the wax.  I would guess also that for such a small bit of wax, Newton's Law of Cooling may be a poor approximation.  This is a case where empirical data may have been helpful, but sadly I did not have my temperature probes and precision heater with me at dinner.

Tea Time

I was making a cup of tea this morning, and started thinking about the various rules I've learned for how to make a good cup.  One of these is that you should never dunk a teabag in and out of the water.  I've certainly found this to be true, but I started wondering why.  My guess is that it causes the solids contained in the tea leaves to dissolve too quickly, and in the wrong proportions.  Dissolution is governed by the equation

where dm/dt is the rate of dissolution, A is the surface area of the dissolving solid, D is the diffusion coefficient, d is the thickness of the boundary between liquid and solid, Cs is the concentration of material on the surface of the solid, and Cb is the concentration of material in the bulk of the liquid.

By dunking the teabag, or otherwise mixing things, you lower Cb near the teabag, causing the rate of dissolution to increase.  Normally, it would take time for the concentration near the teabag to diffuse outward to the rest of the cup, but instead you're doing the diffusion work yourself, speeding things up.

Thinking about this reminded me of an essay by one of my favorite authors, Douglas Adams.  He theorized that "the Americans are all mystified about why the English make such a big thing out of tea because most Americans HAVE NEVER HAD A GOOD CUP OF TEA."  He doesn't mention the dunking issue, but he does give excellent instructions for making good tea.

Works in Progress

Sorry for the long silence; I've been working on a couple different posts, and both have run into problems.  I'm going to be heading off to Swarthmore this weekend for Senior Week and Commencement, so I'm not sure if I'll have a chance to finish anything, but I thought I'd tell you a bit about what I've been thinking about, in case you want to express an opinion about which I should finish first.

Remote Controls - I was watching some TV a couple days ago, and it got me thinking about the way remotes work.  The questions that came to mind were: How many times can the beam bounce off the walls, and still produce a usable signal?  How long does a single command last?  How much could the signal spread out, and still be usable?  I started doing the calculations, but I ran into problems trying to sort out the weird units involved.  (Lumens per steradian?  Seriously?)

Weather Interpolation - Steve runs an electronic weather station in Ashfield that uploads its data to a site called Weather Underground.  I thought it would be interesting to try taking various data from the site (such as temperature) and interpolating between nearby stations to determine the approximate weather in places that didn't have a station.  I've been trying to automate the process with a Perl script, but it's been too long since I did any programming aside from Matlab's insane scripting language, so I'm having some trouble.

Let me know in the comments if one these piques your interest, or feel free to suggest your own idea.

Hammertime

Last Friday, Steve and I went to see the movie Thor.  It was a lot of fun, but Steve keeps insisting the movie was about physics, so I figured I should do a post on it.

One of Thor's powers is that he can use his hammer, Mjöllnir, to fly.  He does this by essentially throwing the hammer, but not letting go, so that it carries him along with it.  My first instinct was that this wouldn't work, but I figured I should go through the mechanics, just to be sure.  Let's say he holds the hammer at his side, and swings it up in a circular arc until it's above his head.  He'll be able to accelerate it until it's straight in front of him, but after this point it will begin to lift him.  Lets say at this point it's moving at a velocity v.  If the hammer has mass m and Thor's arm is of length r, then the force required to maintain it's circular motion is

Once the hammer reaches this point, Thor won't be able to add more energy to it, so let's look at what happens after this.  The lifting force from the hammer will be

where θ is the angle of Thor's arm above horizontal.  If Thor's mass is M, then his upward acceleration will be

θ is a function of time, so we can put it in terms of other variables we have.

Integrating this over the arc will give the velocity of Thor when he finishes the swing.

or a kinetic energy of

That means he could rise to a height of

To get an idea of what this means, let's get some numbers. We'll assume Thor has an average weight of 70 kg.  A quick search for sledgehammers shows a typical weight is about 7 kg.  It's a little tougher to figure out the speed.  I searched around a bit for info, but the best I came up with was this video of a guy swinging a club of similar weight.  He manages about 1 round per second, which translates to a velocity of about 6 m/s.  Thor's a god, so let's estimate he can manage more than double this, and call it 15 m/s.  Plugging all this in gives h = 11.5 cm.  Of course, if we assume Thor has truly god-like strength, then he can swing Mjöllnir as fast as he wants, or we could assume Mjöllnir is stunningly heavy.  Either way, he could manage flight, but it's certainly outside the abilities of any human.

There was one physics detail that really bugged me in the movie.  For much of the film, Mjöllnir is wedged in the ground out in some desert, with a government research team surrounding it.  Occasionally, the team's computers flicker, which they explain is the result of powerful electromagnetic energy being released by the hammer.  What bugs me is that none of them think to simply erect a Faraday cage around it.  Faraday cages absorb electromagnetic waves, and are often used in labs to protect equipment from volatile experiments.  Swarthmore's plasma physics lab uses one to protect their computers from the powerful waves emitted by their spheromak.  You may think I'm being petty, but I feel strongly that if a movie is actually going to talk about science, they should get it right.

PM's Question Time

I thought I'd take a moment again to answer some of your questions...

Carrie asked about this post, "Having never heard of a Fresnel prism before, I was hoping you would write (and post a photo) about it!"
I'm not too clear on how the prism bit fits in, but I know they're related to Fresnel lenses.  Normally, for a certain magnification, you need a certain thickness of lens.  For large magnifications, the thickness can become prohibitively large, so Augustin-Jean Fresnel developed a method to get the large magnification without the large lens.  Rather than shaping the lens as a single curved surface, you divide the lens into zones.  Each zone has the same overall curvature, but they are discontinuous, allowing a large amount of material to be left out.  Here's a schematic (from Wikipedia):

The two lenses have the same magnification, but the Fresnel lens (1) is significantly thinner than the traditional lens (2).  My guess is that the same principle can be applied to prisms – a single prism would need to be excessively thick to accomplish the correct shift distance, so instead it's divided into many smaller prisms.

Chris asked about this post, "Speaking of quantum mechanics, what about laser speckle? When a coherent beam of light scatters off of a rough surface, you get an interference pattern whose intensity varies randomly in the quantum mechanical sense. Theoretically you could inspect tiny areas and get random numbers. Maybe hard in practice.  Can nonlinear phenomena at macroscopic scales give you random numbers?"
Neat idea, Chris, I think laser speckle could work just fine.  When I used to do quantum dot research, the lab was often filled with scattered light from the green laser we used.  When it hit the walls, it had a very clear speckling.  As it happens, I still have a picture.

As for your second question, I'm not sure why not.  Did you have a possible counter-example in mind?

Nate commented on this post, "I think that assuming that the car body is perfectly rigid is a big factor in the low speed you're seeing. The first few things to hit the ground should crumple and increase drag."
I'm not sure whether that would make much difference actually.  Normally, friction doesn't depend on the surface area in contact.  It's quite possible that the normal model for friction doesn't work well in this case though, since the axle could dig into the pavement (acting even more like a pole vaulter).  Even if the real minimum speed is as much as 60 mph though, it's still a speed that people drive at.

Thanks once again for the questions/comments.  I'm thinking this sort of thing will have to be a regular feature...

And the Joker Got Away

A couple weeks ago, I was in the car with Steve and we passed a truck broken down on the side of the road.  It had lost a wheel, and Steve commented that if that happens to a car moving fast enough, it can often flip over.  I was curious exactly how fast the car would need to be going, so I decided to model the situation.

When a front wheel falls off a car, it will tip over slightly, since most of the weight is under the hood.  Suppose the car's axles are a height h off the ground, and the center of mass of the car is a distance d forward from its geometrical center.

The offset of the center of mass will create a torque when the wheel falls off

where w and l are the width and length of the car, and m is its mass.  We're interested in the downward force this creates where the axle touches the road,

The friction from this contact point will tend to slow that corner of the car, but not all of that force will be transferred to the center of mass.  Because the center of mass is higher than the road surface, some of the force will cause the car to lift (think of a pole vaulter turning their forward momentum into lifting power).  The deceleration caused by the friction will be

Some amount of this acceleration will contribute a torque to the center of mass, lifting the car.  If the angle between the axle and the road is θ, then the angular acceleration is

Notice that both θ and h are time-dependent.  By expressing h in terms of θ, we get a differential equation.

where

Unfortunately, there's no easy way to solve this exactly, but by using some typical car dimensions, we can come up with a numerical solution.  I got this diagram from a parking garage manufacturer's site:

Plugging in these numbers, along with a typical coefficient of friction [Link broken. Replacement from Arthur Kirkby], we find for θ(t)

 

but we're only interested in θ up to 90°, since we know at that point the car will flip over.  Solving for this point, we find t = 0.66 s.  That means for the car to flip over, it must still be moving after 0.66 s.  The velocity of the car will be given by

where v0 is its velocity when the wheel falls off, and ax is the acceleration along the road surface.  Using

with the a and θ found above, and solving for v0, we find that the car must be moving at least 4.46 m/s, or about 10 mph.  Surprisingly slow, so maybe some of my assumptions have driven it down from the real speed, but I don't think this is too far off.  In any case, a stern warning to make sure your wheels are in good condition...

Toil and Trouble

One of the first symptoms of my tumor was double vision, since it was putting pressure on my optic nerve.  My doctors had hoped that once the tumor had disappeared, my vision would return to normal, but so far things have been about the same.  Last week, I visited a neuro-ophthalmologist, who prescribed me prisms for my glasses.  I just got them today, and while I'm still on the fence about how much of an improvement they are, I have been enjoying thinking about their physical properties.

 

Notice the faint lines on my lenses.  These are the temporary stick-on Fresnel prisms that were added to my glasses.  If I decided to keep them, they can be ground into my next pair of lenses.  The strength of eyeglass prisms is measured in prism dioptres (Δ).  My prescription is 2 Δ out, and 2 Δ down, meaning an object 100 cm away would appear shifted by 2 cm horizontally and 2 cm vertically.

I have noticed some interesting effects, aside from the intended image shift.  When we were in a grocery store, the strong overhead lights sometimes would reflect only from one section of lens, creating a bright stripe.  I've also found I get some distortion from the lines themselves, and I need to turn my head slightly to avoid looking through one.

I'll spend plenty more time with them before I make up my mind, but my initial reaction is to be a bit disappointed.  I guess I'm just used to the extensive development of normal eyeglass technology, whereas eyeglass prisms are so rarely needed, little improvement has been made.

Triumphant Return

I was released from the hospital yesterday afternoon, and, while I am still a bit nauseous, it's nice to be officially done with chemo.  While I was away, a few of you wrote in questions, either by email or comments, and I thought I'd take a moment to answer them.

Chris asked about this post, "How about getting your equations from the Lagrangian approach?"
Yes, that is a much better idea, and I may do it that way when I come back to this one.  I completely forgot about Lagrange, so thanks for the reminder (and shameful apologies to Matt Mewes if he's reading).  For those who don't know, the Lagrangian approach is an alternative to Newton's methods that is completely equivalent, but often is easier to work out in cases like this, where there are no dissipative forces, like friction.

Jim asked about this post, "Shouldn't velocity enter into the Crr term, thus changing the differentiation? I can't believe you get the same rolling resistance at 20m/s as at 1... And secondly, doesn't part of the force go into changing the wheels' angular momentum?  Do you need a -I*omega term on the right side of that equation?"
Rolling resistance is a bit dodgy, since the whole thing's an approximation anyway, but you're right that using a version that accounts for velocity would have been more accurate.  As far as the angular momentum, I think I'm ok neglecting that in favor of the overall linear momentum.  If you wanted to get into the actual construction of the chairs, you might need to consider it, but assuming everyone has the same design, I think we can do without.

Bob asked about this post, "I read your blog about noise cancellation and was wondering if you could explain how noise cancellation headphones work – I’m assuming they only deal with the problem in two dimensions?  Would it be possible to have two French horns properly situated in relation to an observer so if they blew the same note you would hear nothing? Or do the harmonics make this impossible?"
The key to noise cancelling is that sound is a pressure wave – a series of pockets of high and low pressure.  All you need to do to cancel a sound is absorb the high points, and fill in the low points.  A perfect way to do this is by using the very sound you're trying to cancel, but shifting it slightly so that its low points line up with the original high points, and vice versa.  This becomes more difficult as the frequency increases, since even small misalignments can increase, rather than decrease, the noise.  The timing required can really only be done electronically, so your proposed situation would require robot horn players using identical instruments.

Keep the questions coming; I'll be trying to post often this week to keep my mind off feeling sick.

On Hiatus

I've been low on energy the past couple days, and tomorrow I'll be heading in for my last cycle of chemo, so don't expect new posts for the next week or so.  Feel free to send me suggestions for things to look into once I'm out, either in the comments or by email.  Thanks to everyone who's been reading so far; it makes me happy to see so much interest in science.