I got another lunar question from Papou this week: If the same gun was fired on the Earth and Moon, proportionally, how much further would the bullet travel and would it have a greater velocity?
As I thought about this, there were a couple different effects that could make the bullet go further, so let's see how much each one contributes:
Drag
The most obvious difference between the Moon and Earth is the lack of atmosphere. That will come into a couple of these points, but this is the one most people might think of. When a bullet travels through the air, it needs to push the molecules out of the way. According to Newton, the air will push back on the bullet, creating a drag force:
where ρ is the air density, u is the speed of the bullet, A is the cross-sectional area of the bullet, and cd is the drag coefficient. The drag coefficient depends on the shape of the object, since some shapes are more aerodynamic than others. However, for bullets and other projectiles, people instead use the ballistic coefficient, defined aswhere m is the mass of the bullet. We can combine these to writewhere ad is the drag acceleration. The bullet is slowed down by this drag, meaning it won't get as far before hitting the ground. We can find the ballistic coefficient with tools like this one.
Gravity
Another difference that immediately comes to mind is the difference in gravity: The Moon has about 1/6 the gravity of Earth, which will make the bullet fall more slowly. The bullet's range is limited by how long it takes to hit the ground, so the Moon will allow the bullet to travel further.
Plugging in some typical values shows that the speed increase is pretty negligible.
Putting It All Together
Expansion of Gas
Bullets are propelled down the barrel by expanding gas from the gunpowder. Similar to the drag force above, on Earth air will get in the way. In this case though, rather than drag I think a better model is an opposing pressure on the other side of the bullet. If we assume the bullet has constant acceleration a down the length of the barrel L, then the muzzle velocity is
where P is the pressure from the gunpowder, and P0 is the ambient pressure. Putting everything together, we can get an equation for the muzzle velocity in vacuum based on the one from air:On Earth, the acceleration will be given by
Plugging in some typical values shows that the speed increase is pretty negligible.
Curvature of Body
Since the Earth and Moon are both (approximately) spherical, as the bullet travels, the ground will begin to slope away, increasing the time it takes for the bullet to hit the ground. When I first started thinking about this question, one thing that came to mind was Newton's Cannonball:
 |
| Wikipedia |
As the muzzle velocity increases, the projectile has further to fall, until it reaches orbital velocity and continues falling without hitting the body. For short distances, we can approximate this as
I put together some code to run a simulation of the bullet's flight on Earth and on the Moon, but I ran into some problems with the drag calculation using the ballistic coefficient. I ended up approximating the drag using the drag coefficient for a hemisphere. For the bullet/rifle parameters, I used the numbers from Wikipedia's .22 rifle page, although I also tried cranking up the speed to see the differences. By far, the greatest effect on the range is the decrease in gravity, but drag has some influence, particularly for the higher speed. The curvature has no discernible impact.
In case you're wondering whether a gun would even work on the Moon, Mythbusters tested a pistol in a vacuum chamber, and found that the gunpowder does contain all the necessary chemicals to ignite. In fact, during the Space Race, Russian cosmonauts carried the TP-82 Survival Pistol, reportedly to fend off wildlife in case of crashes in the Siberian wilderness, but you can imagine it was advertised in case American astronauts got any ideas. Thanks for a great question, Papou!
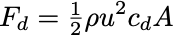








No comments:
Post a Comment