I'm at home in Ashfield for the week, which means I get to spend time with our two dogs, Ida, a yellow lab, and Darcy, a Boston terrier. Both dogs have an interesting habit of wagging their tails so violently that their whole body begins to wag too. I put together a little illustrative animation:
The first thing that came to mind when I saw this was coupled oscillation, when two oscillators are connected, and the movement of one causes the other to begin moving as well.
When dealing with coupled oscillators, it's often useful to find their normal modes. First though, we'll need to come up with some equations that govern this motion. I'm thinking the best model is a sort of angular spring – the more a joint bends, the harder it tries to return to straight. In this case, the equation for the joints would be
where τ is the torque, θ the angle the joint is bent, and k the spring constant. We can turn the torque into a more useful measure of the joints' movement by using the moment of inertia of a rod, I.
where α is the angular acceleration, m the mass, and l the length of the segment of body. In order to use the standard methods for coupled oscillators, we'll need to put this in Cartesian (x and y) coordinates. Since the upper joint is fixed, we'll take as our points of interest the lower joint and the tip of the tail. If we know where these two points are, we can find the positions of everything else. For the lower joint, we have
and for the tip of the tail
so solving for the θs,
We also need the second derivatives of each of these. Starting with the first derivatives,
Then the second derivatives are
Whew, things are looking pretty ugly. I'm going to stop here for now and pick this up again tomorrow. Sorry to leave you hanging...




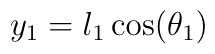





No comments:
Post a Comment