A Con-Vexing Problem

This week in my research I've been trying to produce some figures that will go into a paper on the work I've been doing modeling the LIGO pendulums. The models use a tool from engineering called finite element analysis (FEA), which represent an object as a set of small pieces, called elements, which each have a number of properties assigned to them. For each element, we can calculate the forces applied to it to find how it moves and interacts with the surrounding elements. The problem I was having though was, given a set of these elements that make up a part, how do we find the outline of that part?

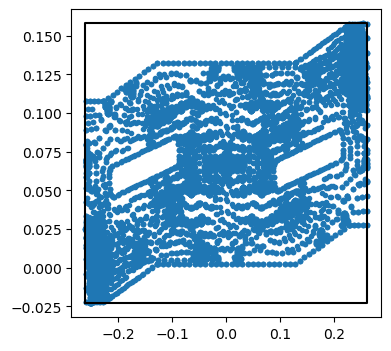
To make things more mathematical, I have a set of points in 2 dimensions (since I'm just looking for a top-down view), and I want to find a closed curve that contains all the points, but has the minimum area. As a zeroth-order approximation, we could just use a box with the minimum/maximum coordinates of all the points as the corners. That doesn't work very well for the set of points I was dealing with though:

Since this stage of the pendulum is tilted in these coordinates, we end up including a lot of empty space. We could do a little better if we rotated our box, but we're still not going to do great with right angles.

Another option is to try to find a convex hull. To get an idea what this looks like, you can imagine stretching a rubber band around the points. One method for finding the path is called the gift-wrapping algorithm, since it touches only the outer-most points, like wrapping a present. The algorithm builds up the path by looking for the largest angle to the next point. Wikipedia has a nice animation of this:

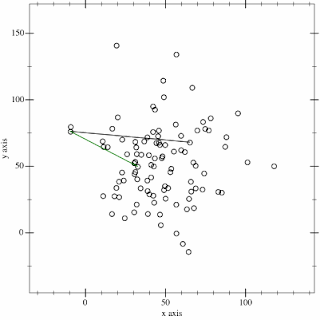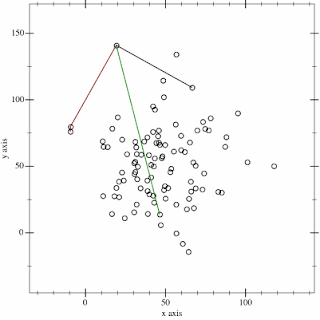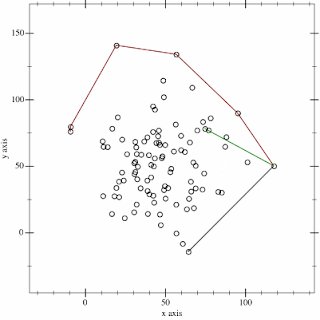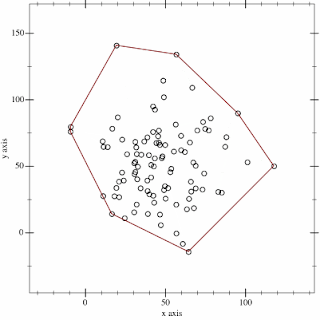Wikipedia

Unfortunately, this only works for convex curves, meaning the shape can't have dents, like our point set does. That brings us to the idea of alpha shapes. These start by dividing the shape into a set of triangles. Each triangle can be assigned a radius based on the size of the circle that would be needed to surround them. We throw out any triangles with radius larger than a given value, then find all the edges that belong to only one triangle – This is the border of our shape. Below are two examples of this for different alpha values, which correspond to the inverse of the radius limit. The red triangles are those that don't pass the limit.

α = 1

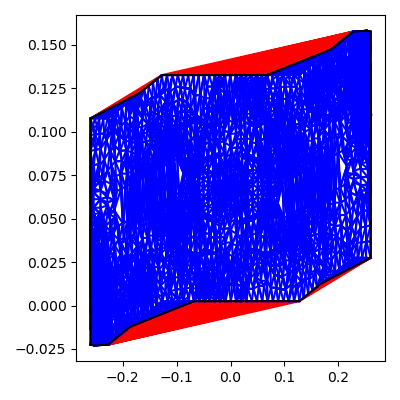α = 2

Below is a comparison of the borders for a couple values of alpha. The first plot is the convex hull, using the Jarvis algorithm, another name for the gift-wrapping algorithm. The second plot, with α = 0, is the same, since that corresponds to an infinite radius, so all the red triangles from above get included.

Once the paper is more complete, I may discuss it here in full, but I'm glad I was able to learn about this technique, so my figures can be a bit more informative.

A Rainbow of Random

Last week I was talking to Steve and Nate (my father and brother), and they mentioned using white noise generators to help with sleeping. That made me think of a meeting I was in earlier in the week where someone mentioned that LIGO and LISA typically have red noise contaminating the measurements. That made me wonder: What does red noise (or other colors of noise) sound like?

First off, we need to talk about what it means for noise to have a particular color. In the context of light, color tells use the frequency of light: red light has lower frequency than blue light, and white light is a mixture of all frequencies. We can apply the same principle to frequencies of sound: more low frequencies is redder, and more high frequencies is bluer. We figure out the "color" of a dataset by taking its Fourier transform, and looking at where the peak frequency lies. White noise has an equal amount of power in all frequencies.

That's the theory, but how do we go about generating different noise colors? White noise is easy: Given some sampling rate, we generate uniformly distributed random numbers. Because these numbers are uncorrelated, they don't favor any frequency, and give a flat spectrum. We can "redden" that noise by giving each sample some dependance on the previous. This page suggests mixing each sample with part of the previous:

where x is the series of samples, w a series of white samples, and r a tuning parameter between 0 and 1, with 0 giving white noise, and 1 giving constant values. For blue noise, we want to do the opposite: sequential values should be as different as possible. To do that we can follow the method here: For each blue point we want to generate, we get several white points and pick the one furthest from a previous sample.

We still haven't gotten to what these different noises sound like though. For that, we can use Javascript's AudioContext, and pipe these sequences of values through your speakers. Below, you'll find a slider to control the color of the noise – For red noise, it represents the r from above, and for blue noise it represents how many samples ago to avoid. That technique isn't quite right, so for values above zero (which is the white noise point) there isn't a continuous transition. In the window above the slider, you can see the Fourier transform of the sound, with the frequency going left to right. Maybe not the most soothing sounds, but I hope it can give you some insight into the sort of problems scientists have to deal with.

Da Breeze of Debris

I recently saw a blog post suggesting publicly available datasets good for testing analysis techniques. Paging through them, I found the US Government's data server included NASA resources, and a connection to my own research occurred to me: One of my colleagues at the University of Florida has been working on simulating the effect of micrometeorite impacts on the LISA spacecraft. At a recent meeting, he was discussing the direction the meteorites might hit the spacecraft – They're generally falling inward toward the Sun, while the satellites (and the Earth) are orbiting around the Sun:

According to this model, very few meteorites should hit from the side facing the Sun. Less obvious though is the other 3 sides: Do more hit the side opposite the Sun, or is there a greater effect from the orbit taking us into the meteorite's path?

NASA's datasets include a record of meteorite landings on Earth, spanning the last 2 centuries, but unfortunately only provides the year, which means we can't find the Earth's position in the orbit. I almost gave up, but then I found a list of Fireball and Bollide Reports, which gives the precise date. Unlike the previous table, these are objects that completely burned in the atmosphere. We can look at the locations where these events were reported, using one of the map projections I discussed a while ago:

These appear fairly evenly distributed, but this plot doesn't consider the location of the Sun. Using the Astropy package, we can find the location of the Sun for a given date, then find the angle from the Sun to Earth, to the direction of the report:

This would seem to suggest that the most common angle is 90°, which corresponds to the orbit taking us into the meteorite. However, there are some significant caveats to this conclusion: It may be that there's a bias in this data, since it's easier to see a streak across the sky, while a meteor coming head-on would just appear as a point. Then there are the limitations of my analysis: The table only give the date of the events, not a time, so I may be introducing bias by choosing midnight. I'll be curious to see what results my colleague turns up, and maybe I'll find more datasets in the list to play with in the future.

Anneal Before Zod

Almost a year ago, I promised to talk about annealing, and now I'm finally getting around to it! I mentioned that you might be more familiar with it than you think, and that's because it's behind something often referred to as the Brazil Nut Effect. I'm not a big fan of mixed nuts, but I do like granola:

Granola will typically have a variety of sizes of cluster, and shaking the bag causes the larger clusters to rise to the top. This happens because the smaller clusters can pack together more densely, and by having those lower in the bag, the system is in a lower energy state. What's interesting is how we got to that lower energy – By shaking the bag, we're adding energy. This seems counterintuitive, but it's the process behind annealing.

If we imagine a potential energy plot like the one I showed a few weeks ago, we can think about how to find the lowest energy state:

We could think about rolling a ball over these hills – We'd like it to settle in the lowest troughs, around 7.5 or 10, but it could get stuck in the ones at 2 and 13, analogous to the large clusters being stuck at the bottom of the bag. To solve this, we can give the ball a temperature, which represents an average velocity. By increasing the temperature, we can get the ball to explore the full range of states, then cool it down gradually to allow it to settle in the lowest-energy position. In the graph below, I've done this with several balls, initially spaced across the full range. The red line shows the temperature, which rises and falls.

A few balls still get trapped in the higher energy states, but the majority find those central troughs. Every time I shake a container to get things to settle, I think about this effect – Maybe now you will too!

Ring Around the 'Rora

Recently I started reading a page called Michigan Aurora Chasers, which shares pictures of the aurora taken in our current home state. The pictures are incredible, but I was really interested by a post that came up discussing Newton's Rings, an effect that can sometimes appear when viewing light from a monochromatic source through a series of lenses, like a camera.

Wikipedia has an example of the effect in a microscope, viewing a sodium lamp:

Wikipedia

For aurora viewers, this happens due to using a flat filter over their curved camera lens. When the light passes through the filter, some will bounce between the lens and filter one or more times, changing the phase. This light can then interfere with the light that passed straight through, producing the dark fringes seen above. The extra distance traveled by the light changes depending on how far from the center of the lens it hits:

The wavelength of light also changes how these rings will appear, since the total phase change from bouncing once from each surface is φ = 4πd/λ, where d is the distance between the filter and lens, and λ is the wavelength. We can scan through the visible wavelengths to see how the pattern of fringes changes (thanks to John D. Cook for the wavelength/RGB conversion):

Due to the spherical shape of the lens, as we get farther from the center, the distance changes more rapidly. This means that if we add up several wavelengths (since true monochromatic light is rare in nature), we see that the rings are only visible near the center of the image, as in the aurora photos from the link at the top:

Our area of Michigan is a bit too far south to get to see the aurora in our own sky, so it's been great to get to see the amazing pictures the group members post. On top of that, they introduced me to this really neat optical effect – Thanks Michigan Aurora Chasers!