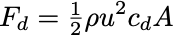Moonshotgun

I got another lunar question from Papou this week: If the same gun was fired on the Earth and Moon, proportionally, how much further would the bullet travel and would it have a greater velocity?

As I thought about this, there were a couple different effects that could make the bullet go further, so let's see how much each one contributes:

Drag

The most obvious difference between the Moon and Earth is the lack of atmosphere. That will come into a couple of these points, but this is the one most people might think of. When a bullet travels through the air, it needs to push the molecules out of the way. According to Newton, the air will push back on the bullet, creating a drag force:

where ρ is the air density, u is the speed of the bullet, A is the cross-sectional area of the bullet, and cd is the drag coefficient. The drag coefficient depends on the shape of the object, since some shapes are more aerodynamic than others. However, for bullets and other projectiles, people instead use the ballistic coefficient, defined as

where m is the mass of the bullet. We can combine these to write

where ad is the drag acceleration. The bullet is slowed down by this drag, meaning it won't get as far before hitting the ground. We can find the ballistic coefficient with tools like this one.

Gravity

Another difference that immediately comes to mind is the difference in gravity: The Moon has about 1/6 the gravity of Earth, which will make the bullet fall more slowly. The bullet's range is limited by how long it takes to hit the ground, so the Moon will allow the bullet to travel further.

Expansion of Gas

Bullets are propelled down the barrel by expanding gas from the gunpowder. Similar to the drag force above, on Earth air will get in the way. In this case though, rather than drag I think a better model is an opposing pressure on the other side of the bullet. If we assume the bullet has constant acceleration a down the length of the barrel L, then the muzzle velocity is 

On Earth, the acceleration will be given by

where P is the pressure from the gunpowder, and P0 is the ambient pressure. Putting everything together, we can get an equation for the muzzle velocity in vacuum based on the one from air:

Plugging in some typical values shows that the speed increase is pretty negligible.

Curvature of Body

Since the Earth and Moon are both (approximately) spherical, as the bullet travels, the ground will begin to slope away, increasing the time it takes for the bullet to hit the ground. When I first started thinking about this question, one thing that came to mind was Newton's Cannonball:

Wikipedia

As the muzzle velocity increases, the projectile has further to fall, until it reaches orbital velocity and continues falling without hitting the body. For short distances, we can approximate this as 

Putting It All Together

I put together some code to run a simulation of the bullet's flight on Earth and on the Moon, but I ran into some problems with the drag calculation using the ballistic coefficient. I ended up approximating the drag using the drag coefficient for a hemisphere. For the bullet/rifle parameters, I used the numbers from Wikipedia's .22 rifle page, although I also tried cranking up the speed to see the differences. By far, the greatest effect on the range is the decrease in gravity, but drag has some influence, particularly for the higher speed. The curvature has no discernible impact.

In case you're wondering whether a gun would even work on the Moon, Mythbusters tested a pistol in a vacuum chamber, and found that the gunpowder does contain all the necessary chemicals to ignite. In fact, during the Space Race, Russian cosmonauts carried the TP-82 Survival Pistol, reportedly to fend off wildlife in case of crashes in the Siberian wilderness, but you can imagine it was advertised in case American astronauts got any ideas. Thanks for a great question, Papou!

The Terror of Knowing What's Inside This Pot

Marika and I recently got an Instant Pot pressure cooker, which we've been enjoying making meals with. Naturally, I was curious about the inner workings of the pot, specifically how the temperature and pressure inside vary with time.

The concept behind a pressure cooker is that when cooking food in water, you typically can't heat it beyond the boiling point: Once the water reaches boiling, any energy you add just goes into making steam. Sometimes you want to cook things at higher temperatures, which is why frying uses oil. That's not very healthy, though, so it would be great to raise the boiling of water. You can do that a little bit by adding salt, which is often suggested for pasta, but that doesn't go quite far enough. Instead, you can put the water under pressure, which raises the boiling point.

A pressure cooker is a sealed container that you add water to, and then heat. As the water evaporates, the pressure builds inside the cooker, raising the boiling point. The pressure depends both on the temperature of the steam, and the number of water molecules that have evaporated:

This is the ideal gas law, with T the temperature in Kelvin, V the volume, R a constant, and n the number of moles of gas molecules. A mole is a way to count very large numbers of things, equal to Avogadro's number, 6.022 * 10^23. My grandfather, a chemist, used to say that he and my grandmother had "Avogadro's Anniversary", because they were married on 10/23.

In order to add molecules to the steam though, we need to boil the water. The temperature that water boils at will change as the pressure increases. Even after we get to boiling, we need to overcome the latent heat to get the water out of the liquid phase and into steam. To accomplish either of these goals, we need to add energy to the system, which translates into temperature through the heat capacity.

Putting all this together with the specs of our model, we can look at the temperature and pressure for two cases: The minimum amount of liquid in the pot, 2 cups, and about half-full, 12 cups.

I was surprised by how quickly the pressure rises once we hit boiling – I kept a constant amount of power throughout the calculation, which causes the pressure to quickly exceed the working range of the pot. You can see the extra energy being used to push more molecules into steam in the sudden change in slope of the temperature plots.

I was hoping that by studying pressure cookers a bit more closely, I'd find them less terrifying to use, but I'm not sure these results are very soothing! I'll just have to keep singing to myself, "Mm ba ba de, Um bum ba de, Um bu bu bum da de..."

Vault of Secrets

I'm still here! I've missed posting the last few weeks thanks to a couple trips to visit family, and some home improvement projects, but things have settled down, and I finally have a weekend where I'm not too exhausted to come back here. This weekend, Marika and I have been watching some Olympics results, and seeing Katie Nageotte's gold medal-winning vault reminded me of something I've wanted to look into: the Fosbury Flop.

Popularized in the 1986 Olympic high jump by Dick Fosbury, the Flop is a clever bit of physics that lets an athlete jump over a bar, despite their center of mass going under it. That means that they can clear a greater height than their speed would normally allow. By bending their body over the bar, the jumper can keep most of their weight below it. This diagram from Wikipedia is helpful:

Wikipedia

I wondered whether I could see if Nageotte was able to benefit from the same sort of trick. I took a few frames from the video linked above, and picked some key points on her body: head (blue), arms (red), torso (green), legs (yellow), and a point on the bar (black).

Once again using that creepy Air Force document listing body part masses that I used for the chicken-slapping post, we can find Nageotte's center of mass:

This says that the position of the center of mass is the weighted average of the positions of all the bits of mass we're adding up. We still need to relate the height of this center of mass to the height of the bar, but that's made difficult by the camera angle: The height in the frame changes as we move horizontally. We know the bar is level at 4.9 m though, so we can use its endpoints to draw a line relating the horizontal and vertical positions. Putting everything together, we can find Nageotte's center of mass relative to the bar:

Based on my estimates, her center of mass did clear the bar, but by less than a foot! I'm not much of a sports fan, but I still am impressed by the feats performed by these athletes. Congratulations to all the Olympic contenders!