Fermat's principle states that light will take the path between two points that minimizes the time, rather than the distance, required to travel between them. In most cases, light simply moves in a straight line, but when it moves from one material to another, it refracts, bending its path according to the properties of the two materials. The important factor is the difference in refractive index, a number determined by the material's molecular structure, conductivity, and other properties. Vacuum has a refractive index of 1, and air is quite close, with 1.0003. However, water has a refractive index of about 1.33. This is why objects appear shifted when you dip them partway into water.
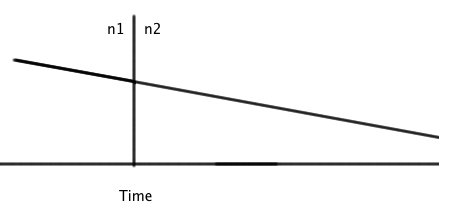
It might seem perplexing that this shift has anything to do with the speed of light, but it's a little clearer looking at a diagram. If we plot the light's path according to position, it will look like this:
The shortest distance between two points is a straight line, so this certainly doesn't look right. However, if we instead plot according to time, taking the speed of the light into account,
The light moves more slowly in the second material, so we stretch out the line we had. Looking at it this way, it's much clearer why the light is bent in space.
I always enjoy making these write-ups, and I'm sure it's good practice, so I'll be back here as often as my workload allows. As always, questions are welcome, on this or any of the older posts.


Hooray for the return of FF!
ReplyDeleteI like your graphs, but I'm having trouble mapping them to the picture of refraction. How is the refracted image taking a shorter path?
And if it takes longer for light to travel through water, does that mean that when I see a spoon in a glass, the part inside the water is actually further back in time than the image of the part above the water?
Was this based on Uttam's question? That Principle of Least Action lecture was rather elegant.
ReplyDeleteAnyway I enjoy reading these posts. Will look forward to the next one. (I have a suggestion - maybe you want to tackle Bell's Inequalities sometime? Those are always interesting).
--Michelle