The Great Mubbet Caber

I may have mentioned before that I'm a big fan of the British quiz show QI. A recent episode included a discussion of an event from the Scottish Highland Games, the caber toss. In the sport, competitors must throw what amounts to a tree trunk such that it flips end-over-end and lands pointing as straight as possible away from them. You can see a video with some examples here:

I was really curious about the physics involved in determining a successful flip. I decided to make a simplified model of the sport: The competitor holds the caber at an initial angle θ, measured from the horizontal behind them. Then they run forward up to a speed v, and stop, exerting a torque on the end of the caber. It continues forward, while beginning to spin. When one end touches the ground, it sticks, and then the initial speed and gravity determine which direction it falls.

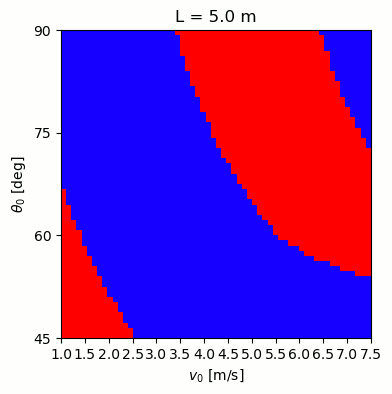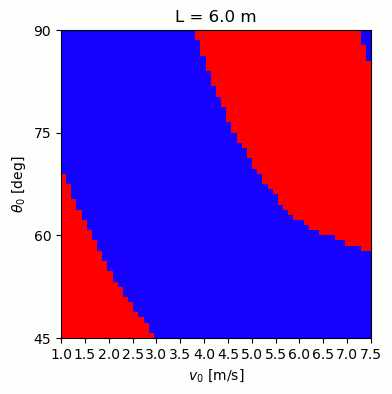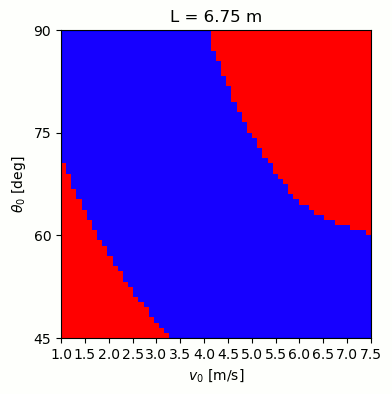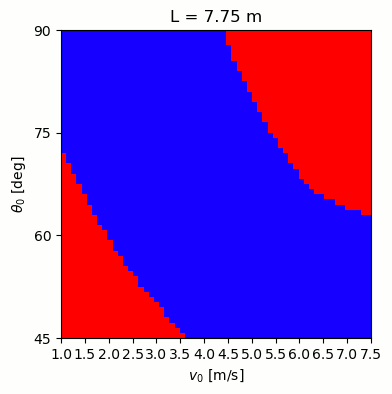
Based on the Wikipedia article I linked above, I tried a range of different lengths (5-7.75 m), angles (45-90°), and initial velocities (1-7.5 m/s or 2-17 mph). For each case, I ran the simulation and tested whether the caber fell away, or back toward the athlete. The plots below show the results, with blue indicating success, and red failure. As the length changes, the successful ranges shift, and for the shortest cabers they can even flip twice (blue region in the upper right)!

For the longest case, I also animated the throws for the 4 corners: min/max speed and angles:

As with many of these posts, I'm not sure understanding the theory would make me any more able to compete, but I'm content to use my imagination!