As I went to get some shampoo in the shower earlier this week, I had a familiar experience: The bottle was running low, so we stored it upside down. Sometimes the air trapped inside is at a higher pressure than the surrounding air, which causes shampoo to be forced out by the extra pressure. Normally, I'd stop this by squeezing the bottle in a way to suck the shampoo back in, but the brand we have right now uses bottles with a circular cross-section, so that didn't work. It did get me thinking about how the right geometry lets me control the pressure inside the bottle.
Most of the shampoo bottles I've used in the past have had a cross-section that's roughly elliptical, which have an area of
We need to choose a precise relationship between a and b – I decided the ellipse should have a constant perimeter. That can be calculated with
Unfortunately, there's no closed-form solution for this, so instead I set up a Python script to calculate it. The pressure in the bottle will be inversely proportional to the volume, which for any cylindrical shape is just the area times the height, so we can write
where p and A are the initial pressure and area. Now, given a change in a, we can find the value of b that keeps the perimeter constant, then get the area, and then the change in pressure. Using a fixed value of 1 for the initial b size, we can try a couple different values for the initial a size to see how they react to squeezing:
Increasing the width by squeezing along the smaller axis always increases the pressure, which makes the shampoo come out of the bottle. The wider the large axis is, the more difference squeezing it makes, but if a = b = 1 like the bottles we were finishing, then any amount of squeezing will increase the pressure, resulting in too much shampoo!

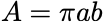




No comments:
Post a Comment