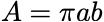Putting the Squeeze on 'Em

As I went to get some shampoo in the shower earlier this week, I had a familiar experience: The bottle was running low, so we stored it upside down. Sometimes the air trapped inside is at a higher pressure than the surrounding air, which causes shampoo to be forced out by the extra pressure. Normally, I'd stop this by squeezing the bottle in a way to suck the shampoo back in, but the brand we have right now uses bottles with a circular cross-section, so that didn't work. It did get me thinking about how the right geometry lets me control the pressure inside the bottle.

Most of the shampoo bottles I've used in the past have had a cross-section that's roughly elliptical, which have an area of

where a and b are the half-width, and half-height. If I squeeze on the longer axis, I can shrink a and expand b, which changes the area:

We need to choose a precise relationship between a and b – I decided the ellipse should have a constant perimeter. That can be calculated with

Unfortunately, there's no closed-form solution for this, so instead I set up a Python script to calculate it. The pressure in the bottle will be inversely proportional to the volume, which for any cylindrical shape is just the area times the height, so we can write

where p and A are the initial pressure and area. Now, given a change in a, we can find the value of b that keeps the perimeter constant, then get the area, and then the change in pressure. Using a fixed value of 1 for the initial b size, we can try a couple different values for the initial a size to see how they react to squeezing:

Increasing the width by squeezing along the smaller axis always increases the pressure, which makes the shampoo come out of the bottle. The wider the large axis is, the more difference squeezing it makes, but if a = b = 1 like the bottles we were finishing, then any amount of squeezing will increase the pressure, resulting in too much shampoo!

A Breath of Fresh Vacuum

This past week was LISACon 8, a meeting of the LISA Consortium, similar to the LIGO meetings I've attended in the past. One of the presenters showed this daVinci-esque drawing of the LISA constellation:

ESA

A couple weeks ago, I talked about how I was working on a model of the rotation of the LISA satellites. Nominally, the satellites form an equilateral triangle, with 60° angles, but over the course of a year's orbit, those angles "breathe", getting wider and narrower as the spacecraft move along their orbits. That means that we need to change the angles the lasers point, so they can hit the distant sensors.

The laser beams are sent and received by Movable Optical Sub-Assemblies (MOSAs), the tubes in the picture above. We need to rotate those MOSAs to track the other satellites, but there's a problem: Angular momentum is conserved. Usually, we can count on the Earth to absorb extra angular momentum, but that's not possible in orbit. When we turn one of the MOSA, the spacecraft will turn under it. We can figure out how much using Newton's laws:

This says that the sum of the torques on each MOSA and the body of the spacecraft have to cancel out – "Every action has an equal and opposite reaction." We can use another of Newton's laws to express those torques in terms of the angular acceleration:

Here, the Is are the rotational inertia of the MOSAs and the spacecraft. The accelerations are measured in the inertial frame where all three bodies are rotating, but the MOSAs move within a range on the spacecraft, so we really want relative accelerations. We can get this by regrouping things:

We can make a bare-bones model by imagining two rods rotating in a solid disk to get I_M and I_S, then integrate to get the angles:

where m_S and m_M are the masses of the spacecraft and each MOSA, and φ1 and 2 are the angles of the MOSA relative to the spacecraft.