Sowing Division

We have several recipes that make 6 servings, and I always have a hard time dividing them equally. It seems I have an easier time splitting things in 2 rather than 3 or other divisions – I assumed this was a human tendency, but I can't turn up anything from searches. While cutting up a casserole one evening, I started thinking about how after cutting 1/3, the next cut would be half of 2/3. Instead of making that cut, I could mark the half and then flip the relation: I have a new 1/3, and I can split the remaining 2/3 in half.

We can put this idea in more mathematical terms: I want to place points a and b on a line of length 1 so that a = 1/3 and b = 2/3, but I can only put them at halfway points. If we start with a0, then b0 goes at (1 + a0)/2. If we keep going back and forth, then

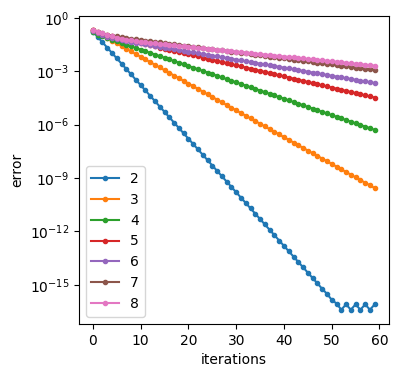
Writing out the first few terms of the sequence for a lets us identify it:

The term in the parentheses is a geometric series, which can be replaced with a simple form. After some rearranging, we get

I realized this technique could be applied to any number of cuts by adjusting each to the center of the two neighboring cuts. Finding an expression for the general case is "left as an exercise to the reader" (textbook cop-out) – I just tossed the algorithm into Python. The main thing I was interested in was how long it takes to get an accurate estimate of the divisions, so I plotted the RMS error at each step:

Each line represents a different number of cuts. Notice that the y scale is logarithmic, meaning these straight lines actually represent exponential decreases. The line for 2 cuts into 3 pieces drops so quickly, it appears to run into some precision error. As the number of cuts increases though, the error is much more difficult to reduce. To get a more concrete handle on this plot, I also made an animation of the cuts as we make iterations:

For the first step, the divisions are evenly distributed at the two endpoints, which is really a worst case scenario. However, we can see how quickly the 2 cuts on the first line settle in place. Moving up the plot, each line takes a little longer to stabilize.

I'm not sure my serving-precision needs are high enough to require actually using this technique, but it was interesting to think through!