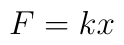(Another old t-shirt design. Credit goes to my dear friend Jen Trinh for the wonderful Einstein drawing.)
Tomorrow I'm heading off for a trip around the East to visit friends and family before I disappear into Michigan for grad school. I probably won't be posting anything here for about a week, but the long train ride ahead of me got me thinking about the possibility of high-speed travel to other solar-systems. I wondered about the relativistic effects of my own travel – my train ride shouldn't actually feel like 6 hours, since I'll be moving.
In special relativity, traveling at a velocity v causes time to slow by a factor of
The faster Amtrak trains average about 63 mph, giving γ = 1 + 4.4 x 10^(-15). That means that while my trip may last 6 hours, it will feel 95 picoseconds shorter than that. What a timesaver!
Wednesday, July 27, 2011
Monday, July 25, 2011
Zip Line and Sinker
Earlier today, Steve and I went to see Captain America. It was very entertaining, but as usual, I have a physics nitpick. In one scene, the Captain and his men ride a zip line down from a mountaintop and drop off onto a speeding train, landing with ease. It seems to me it would require an enormous height difference to achieve the necessary speed to land on the train without being thrown off.
We can find the height necessary to achieve a certain speed using energy. The kinetic energy gained by dropping a height h is
where m is the object's mass and g is the acceleration due to gravity. Meanwhile, the energy involved in traveling a velocity v is
Putting these together and solving for h gives
Given the era, I'm guessing the train was a diesel engine, so its top speed would be around 100 km/h. Plugging that into our equation gives 39 meters, or about 13 stories. Also note that this is the minimum height, since it assumes that all his downward momentum gets transferred to horizontal. If the zip line were at a 45° angle, it would require twice the height. Don't let my pedantry put you off though; it was a great movie, well worth seeing.
We can find the height necessary to achieve a certain speed using energy. The kinetic energy gained by dropping a height h is
where m is the object's mass and g is the acceleration due to gravity. Meanwhile, the energy involved in traveling a velocity v is
Putting these together and solving for h gives
Given the era, I'm guessing the train was a diesel engine, so its top speed would be around 100 km/h. Plugging that into our equation gives 39 meters, or about 13 stories. Also note that this is the minimum height, since it assumes that all his downward momentum gets transferred to horizontal. If the zip line were at a 45° angle, it would require twice the height. Don't let my pedantry put you off though; it was a great movie, well worth seeing.
Friday, July 22, 2011
Queen Kong
You may remember a post from early in my blog, when I mentioned our (relatively) new Boston Terrier, Darcy. I referred to her as a volatile dog, but didn't give any details, so I thought I might take a moment to quantify her explosive nature. She enjoys chew toys very much, but we've found that most toys can be destroyed within seconds. Squeaking weasels have been eviscerated, and bones have been chewed into shreds. The one type that has stood up to her has been the Kong, a chew toy inspired by a part of the suspension of a VW van. It's shaped as a conical tube, which she spends hours a day crushing flat, only to have it spring back. I've tried this myself (with my hands, that is) and it's impressively difficult to do, so I started wondering how many calories she was burning with this jaw exercise.
The only scale we had around was a small kitchen one that only went up to 5 kg, but if we assume the Kong follows Hooke's Law (the usual approximation for a spring) we can figure out the energy involved.
so squeezing the Kong flat (3.61 cm) requires 10.4 J, or 0.0025 Calories. It may not seem like much, but that's about equal to the energy involved in one arm-curl of an 8 pound weight. Also keep in mind that Darcy is only 18 pounds herself, so imagine lifting half your own weight. I should also note that, if anything, this is an underestimate, since it feels to me as if it gets more difficult to compress as it flattens. Further evidence that Darcy is not a dog to cross...
The only scale we had around was a small kitchen one that only went up to 5 kg, but if we assume the Kong follows Hooke's Law (the usual approximation for a spring) we can figure out the energy involved.
Measuring the larger opening closest to the camera, the difference between the uncompressed Kong (left), and the Kong compressed by 4.2 kg (right) is 0.26 cm. Hooke's Law gives the force exerted by a spring compressed a distance x as
where k is a constant that characterizes the strength of the spring. Using the information we have, k = 16,000 kg/s^2. The energy required to compress a Hooke's Law spring isso squeezing the Kong flat (3.61 cm) requires 10.4 J, or 0.0025 Calories. It may not seem like much, but that's about equal to the energy involved in one arm-curl of an 8 pound weight. Also keep in mind that Darcy is only 18 pounds herself, so imagine lifting half your own weight. I should also note that, if anything, this is an underestimate, since it feels to me as if it gets more difficult to compress as it flattens. Further evidence that Darcy is not a dog to cross...
Thursday, July 21, 2011
Raise a Glass
Last night, we drank champagne to celebrate the end of my treatment. The flutes we used got me thinking about the old trick of running a wet finger around the rim of a wine glass to make a tone. I wondered whether it would be possible to predict the frequency of the tone based on the shape of the glass. I tried it out on three different glasses:
According to Wikipedia, the resonant frequency of a cone (which we'll approximate the leftmost two glasses as) is the same as that of an open cylinder, which is given by
where n is any positive integer, v is the speed of sound, L is the length of the tube (in this case the height of the inside of the glass), and d is the diameter of the tube (in this case the diameter halfway up the glass). The rightmost glass we'll approximate as a closed cylinder, whose resonant frequency is
I tabulated the results of these equations, and the frequencies I actually measured below:
I'm impressed by how well the results fit the theory, given all the approximations involved. Even a perfect cone or cylinder would not be exactly described by the equations above, but it's nice to see that they work well on even an imperfect example.
According to Wikipedia, the resonant frequency of a cone (which we'll approximate the leftmost two glasses as) is the same as that of an open cylinder, which is given by
where n is any positive integer, v is the speed of sound, L is the length of the tube (in this case the height of the inside of the glass), and d is the diameter of the tube (in this case the diameter halfway up the glass). The rightmost glass we'll approximate as a closed cylinder, whose resonant frequency is
I tabulated the results of these equations, and the frequencies I actually measured below:
| Glass | Small Cone | Large Cone | Flute |
| n | 1 | 1 | 3 |
| L (cm) | 4.62 | 7.61 | 11.3 |
| d (cm) | 7.23 | 7.5 | 5.49 |
| Theoretical Freq. (Hz) | 1914.49 | 1416.18 | 1906.12 |
| Measured Freq. (Hz) | 1850.3 | 1548.9 | 1704.7 |
| Percent Error | 3.47 | 8.57 | 11.82 |
Wednesday, July 20, 2011
The Deed is Done
Today was the last day of my proton radiation therapy. This marks the end of my cancer treatment, though I still have a few check-ups and a lifetime of periodic MRIs ahead of me. I couldn't have made it this far without the incredible support of all my friends and family, but there are a few people that I think deserve special recognition and thanks:
- My optometrist, Brian Wadman, who first noticed my swollen optic nerve and sent me for the MRI that revealed my tumor.
- My neurosurgeon, Ziv Williams, who evidently heeded my warning that my brain is about all I have going for me.
- My oncologist, David Ebb, who planned my treatment and kept a watchful eye over me throughout the ordeal.
- My nurse, Patti Scott, who would smile and laugh with me as she drew tube after tube of blood samples from my chest-port.
- My radiation oncologist, Shannon MacDonald, who was a match for my geekiness as she explained the inner workings of the MGH cyclotron.
- My mother Sally, who kept at work during this difficult time, providing the top-notch health insurance that allowed me to be treated.
- Most of all, my father Steve, who has been my roommate, nurse, chef, personal trainer, secretary, biographer, chauffeur, and friend during the worst 7 months of my life so far.
Tuesday, July 19, 2011
The Tappet Challenge
It seems my brother Nate is becoming a major source of blog material. The other day, he pointed me to NPR's podcast of last Saturday's Car Talk. Near the end of the show (44:38, if you'd like to hear for yourself) the hosts take a call from a woman looking to prove her husband wrong about his driving style. The husband claims that you can get better gas mileage by accelerating up to some top speed, then allowing the car to coast until it slows to a minimum speed, before accelerating once again to the top speed. Click and Clack maintain that, whether or not it really is better for your mileage, any money you save will be outweighed by the damage you do to your car. They invite (or perhaps dread) any physicists listening to send them evidence one way or the other, so here I am.
We'll assume there are only two significant forces on the car: the wind resistance slowing it down, and the car's own acceleration speeding it up. Given this, we can write a differential equation for the car's position:
where a is the acceleration applied by the car, and c is a constant associated with the wind resistance. Solving the equation gives
which is admittedly pretty awful. However, we're not really interested in t, so we can differentiate this to get the velocity, and solve the two equations simultaneously to get
We'd like to know the distance traveled to get from an initial speed vi to a final speed vf. We can find this by taking the difference between the two points:
Now that we have this equation, we can find the distance the car travels during one cycle of accelerating and decelerating. If we call the car's minimum and maximum speeds vlo and vhi, then the distance spent accelerating is
and the distance decelerating is
Using these, we can define an efficiency, ε, analogous to a measure like miles per gallon:
where E is the energy expended in traveling the distance. It will be given by
where m is the mass of the car. Plugging everything in, we have
where
We'd like to compare this to the efficiency of maintaining a constant velocity. First, we need to know the average speed of the accelerating car. Going back to our original differential equation, we can get the time in terms of the change in velocity:
We can use this to find the average velocity with
but the result is pretty awful, so I won't write it out just yet. In this case, our efficiency is given by
so that makes our nasty equation even worse. To spare you the horror, I decided to toss in some dummy values and see what sort of results we get. To get a comparison of the two efficiencies, I divided the constant speed efficiency by the accelerating efficiency, so any values greater than 1 indicate that constant speed is the way to go.
Using the 65/55 speed range they discuss in the show, we get
so it seems Click and Clack were correct in their theory that the husband's method does not save gas. I tried fiddling around with the speeds a bit, and I couldn't find a case where accelerating and decelerating is a good idea. However, these equations I'm using are a real mess, so I can't be sure I've got everything exactly right.
Thanks for another great tip, Nate! I considered closing with, "Don't drive like my brother," but I don't even have a license...
We'll assume there are only two significant forces on the car: the wind resistance slowing it down, and the car's own acceleration speeding it up. Given this, we can write a differential equation for the car's position:
where a is the acceleration applied by the car, and c is a constant associated with the wind resistance. Solving the equation gives
which is admittedly pretty awful. However, we're not really interested in t, so we can differentiate this to get the velocity, and solve the two equations simultaneously to get
We'd like to know the distance traveled to get from an initial speed vi to a final speed vf. We can find this by taking the difference between the two points:
Now that we have this equation, we can find the distance the car travels during one cycle of accelerating and decelerating. If we call the car's minimum and maximum speeds vlo and vhi, then the distance spent accelerating is
and the distance decelerating is
Using these, we can define an efficiency, ε, analogous to a measure like miles per gallon:
where E is the energy expended in traveling the distance. It will be given by
where m is the mass of the car. Plugging everything in, we have
where
We'd like to compare this to the efficiency of maintaining a constant velocity. First, we need to know the average speed of the accelerating car. Going back to our original differential equation, we can get the time in terms of the change in velocity:
We can use this to find the average velocity with
but the result is pretty awful, so I won't write it out just yet. In this case, our efficiency is given by
so that makes our nasty equation even worse. To spare you the horror, I decided to toss in some dummy values and see what sort of results we get. To get a comparison of the two efficiencies, I divided the constant speed efficiency by the accelerating efficiency, so any values greater than 1 indicate that constant speed is the way to go.
Using the 65/55 speed range they discuss in the show, we get
| Acceleration | Ratio |
| 1 | 1.00697 |
| 3 | 1.00697 |
| 5 | 1.00696 |
| 7 | 1.00696 |
| 9 | 1.00696 |
| 11 | 1.00695 |
| 13 | 1.00694 |
| 15 | 1.00693 |
| 17 | 1.00692 |
| 19 | 1.00691 |
| 21 | 1.00688 |
| 23 | 1.00685 |
| 25 | 1.00679 |
Thanks for another great tip, Nate! I considered closing with, "Don't drive like my brother," but I don't even have a license...
Sunday, July 17, 2011
Magneto Goes Back to School
Nate asked me a couple questions about my last post, which I thought I would take a minute to answer.
Can you give a more detailed explanation of magnetic fields with a non-zero second derivative? Can we generate them in a lab? Do they occur naturally?
Yeah, I glossed over that a bit. The idea is that the field can't just be changing – the rate of change must change. As complicated as that sounds, it's actually really easy to do. If you hold a magnet in your hand and move it around, you're making a magnetic field with non-zero second derivative. However, if you wanted to generate even visible light (let alone the deadly ionizing radiation I was talking about) you'd need to move the magnet up and down on the order of quadrillions of times per second. Who knows how quickly Magneto can change his fields, but maybe with a bit of practice he could manage it.
If I have an electromagnet and I vary the input power, would that produce photons?
This may seen like a more reasonable way to get the fast variation that I'm talking about, but now you'll run into the problem of inductance. Electromagnets create magnetic fields from electric current, but when you increase the current in an electromagnet, the magnetic field will also increase. This creates an electric field which opposes the increasing current, slowing things down. The same happens when the current decreases, so you still may not be able to get the speed you need.
And are the photons being produced, or just redirected?
I think it's fine to say that they are being produced, but this is getting into an area of physics I don't know much about yet. Photons are quantum mechanical particles, while electromagnetic fields (at least the sort I'm talking about) are classical approximations of whatever is studied in quantum field theory. Technically, I'm not sure if it's ever correct to say that a photon is 'redirected,' but they can be absorbed and re-emitted in a different direction.
Thanks for more great questions, Nate! Everyone else should feel free to send me their own – part of the purpose of this blog is to educate, so don't feel afraid to ask even the simplest questions.
Friday, July 15, 2011
Magneto Gets an F
Last night I watched X-Men: First Class, and enjoyed it very much; it was far better than I remember the earlier movies being. However, there's something that has always bothered me about the X-Men franchise: it seems Magneto, the mutant who can create powerful magnetic fields at will, never took physics. There's much more he could be doing with his power, aside from tossing metal things around.
Before I get into that, I'd like to figure out exactly how powerful his magnetic fields are. During one scene, he lifts a submarine out of the water and into the air:
A little research suggests that, although this is not a real submarine model, the Type XXI is a good approximation. Using the length of the sub as a scale, we can estimate that the center of the sub (where we'll assume its center of mass is) is about 21 meters above the bottom of the picture. The energy required to lift something to a specific height is given by
where m is the mass of the object, g is the acceleration due to gravity, and h is the height to which it is raised. We can get an underestimate of this energy by assuming the submarine was on the surface of the water when Magneto started lifting it. Plugging in the values we have, it would take 3.3 x 10^8 Joules. I estimate it takes him about 20 seconds to get it there, giving a power output of 1.7 x 10^7 Watts. [Update: I realized that, if that energy is coming from Magneto himself, he must be eating at least 80,000 Calories per day.]
With that in hand, we can turn to other uses of Magneto's power. Maxwell's Equations tell us that changing magnetic fields induce electric fields, the simplest application of that being to create currents in conductors. However, if he can create 'accelerating' magnetic fields (ones with non-zero second derivative), he can shoot lasers. Light is made up of oscillating electric and magnetic fields, and since each induces the other, you only need one to get things started. If he could manage to produce gamma rays (a dangerously high-energy variety of photons), according to our power output calculated above, he'd be putting out 8.6 x 10^20 photons/second. That's about on the order of how many photons a lightbulb produces, but we're talking about a lightbulb putting out lethal radiation.
I suppose it wouldn't make for a very interesting story if Magneto simply gave everyone on Earth radiation poisoning, so maybe the writers are justified in ignoring this possibility. It still would have been better than this possibility.
Before I get into that, I'd like to figure out exactly how powerful his magnetic fields are. During one scene, he lifts a submarine out of the water and into the air:
A little research suggests that, although this is not a real submarine model, the Type XXI is a good approximation. Using the length of the sub as a scale, we can estimate that the center of the sub (where we'll assume its center of mass is) is about 21 meters above the bottom of the picture. The energy required to lift something to a specific height is given by
where m is the mass of the object, g is the acceleration due to gravity, and h is the height to which it is raised. We can get an underestimate of this energy by assuming the submarine was on the surface of the water when Magneto started lifting it. Plugging in the values we have, it would take 3.3 x 10^8 Joules. I estimate it takes him about 20 seconds to get it there, giving a power output of 1.7 x 10^7 Watts. [Update: I realized that, if that energy is coming from Magneto himself, he must be eating at least 80,000 Calories per day.]
With that in hand, we can turn to other uses of Magneto's power. Maxwell's Equations tell us that changing magnetic fields induce electric fields, the simplest application of that being to create currents in conductors. However, if he can create 'accelerating' magnetic fields (ones with non-zero second derivative), he can shoot lasers. Light is made up of oscillating electric and magnetic fields, and since each induces the other, you only need one to get things started. If he could manage to produce gamma rays (a dangerously high-energy variety of photons), according to our power output calculated above, he'd be putting out 8.6 x 10^20 photons/second. That's about on the order of how many photons a lightbulb produces, but we're talking about a lightbulb putting out lethal radiation.
I suppose it wouldn't make for a very interesting story if Magneto simply gave everyone on Earth radiation poisoning, so maybe the writers are justified in ignoring this possibility. It still would have been better than this possibility.
Thursday, July 14, 2011
Singing Pavement
With all the highway travel I've been doing, I've started noticing little differences in the roads. One aspect that has always interested me is the way the sound of the car changes depending on the type of pavement. I decided to try to get a quantitative picture of the changes on our way out of Boston today. I grabbed a frequency analyzer for Steve's iPad and took some samples when we were driving on a recently paved road, an old worn road, and a soon to be paved, milled road. The milled road wasn't very long, so I only managed to grab one sample.
In order to account for the varying speed of the car, I decided to define a characteristic length: the car speed divided by the dominant frequency of sound. I'm not sure what this length means exactly, but it's useful as a way to compare. Here are my results:
It seems the characteristic length increases as the quality of the pavement decreases. This makes me think the length may be related to the average distance between bumps or pits in the road, but I'm sure it's more complicated than that.
In order to account for the varying speed of the car, I decided to define a characteristic length: the car speed divided by the dominant frequency of sound. I'm not sure what this length means exactly, but it's useful as a way to compare. Here are my results:
| Pavement Type | Car Speed (m/s) | Dominant Frequency (Hz) | Characteristic Length (cm) |
| New | 29.5 | 235.7 | 13 |
| New | 30.8 | 126 | 24 |
| New | 31.7 | 334.6 | 9 |
| New (Average) | 30.7 | 232.1 | 15 |
| Old | 31.7 | 150.2 | 21 |
| Old | 30.8 | 289.9 | 11 |
| Old | 31.3 | 161.7 | 19 |
| Old (Average) | 31.3 | 200.6 | 17 |
| Milled | 27.3 | 137.1 | 20 |
It seems the characteristic length increases as the quality of the pavement decreases. This makes me think the length may be related to the average distance between bumps or pits in the road, but I'm sure it's more complicated than that.
Monday, July 11, 2011
Newtonian Granita
Last night I made some Watermelon Granita, but the pan I used to freeze it was smaller than the recipe called for. It got me thinking about how the dimensions of the pan affect the rate of freezing.
Assuming we have a rectangular pan, the volume is simply
and the surface area is
In comparing pans, we'll want the same volume, so we can combine these to eliminate a dimension:
According to Newton's Law of Cooling, the difference in temperature between the pan and the surrounding air in the freezer will be given by
where r is defined as
and h is the heat transfer coefficient, m is the mass of the substance being cooled, and cp is the specific heat capacity of the substance.
We're interested in how long it takes the granita to freeze, so solving Newton's equation for t gives
Notice that the only thing that will change with the container dimensions in this equation is A, so for any pair of containers, we can write
This is a surprisingly simple equation – a pan of half the area will take twice as long to freeze. This isn't perfectly accurate, since Newton's Law of Cooling is an approximation, but I still expected something much more complicated.
Assuming we have a rectangular pan, the volume is simply
and the surface area is
In comparing pans, we'll want the same volume, so we can combine these to eliminate a dimension:
According to Newton's Law of Cooling, the difference in temperature between the pan and the surrounding air in the freezer will be given by
where r is defined as
and h is the heat transfer coefficient, m is the mass of the substance being cooled, and cp is the specific heat capacity of the substance.
We're interested in how long it takes the granita to freeze, so solving Newton's equation for t gives
Notice that the only thing that will change with the container dimensions in this equation is A, so for any pair of containers, we can write
This is a surprisingly simple equation – a pan of half the area will take twice as long to freeze. This isn't perfectly accurate, since Newton's Law of Cooling is an approximation, but I still expected something much more complicated.
Friday, July 8, 2011
Having a Ball
As a graduation present, Amy Bug (one of my Swarthmore physics professors) gave me an interesting little desk toy:
It's a rubber ball filled with a thick liquid, some glitter, and a smaller ball containing some LEDs and an accelerometer. When the accelerometer detects that the ball has bounced, it starts blinking the LEDs for a few seconds. I've found that a quick wrist-flick can also trigger them. What I'd like to talk about here though is what happens when the ball spins:
I would have expected the glitter to tend toward the widest part of the ball, the center, but instead it fills the whole thing.
We'll assume that the thick liquid makes the force of gravity negligible, much like in the Neutral Buoyancy Laboratory used by NASA. That just leaves the normal force that the sides of the ball apply to the glitter. The radial component of this force will be related to the rotation of the ball by
where m is the mass of the glitter, r is the radius of the ball at a particular height, ω is the angular velocity of the ball's rotation, and N is the normal force. Since the ball is spherical, we can express r in terms of the height, z:
where R is the radius of the ball at its center. Using this, we can express the slope of the wall in terms of z as well:
This gives the direction of the normal force as
so putting this into our original equation and solving for N gives
Now that we have a general equation for N, we can find its z component:
Since we're assuming that the normal force is the only force on the glitter, we can write
Solving this differential equation with the initial condition z(0) = z'(0) = 0 gives
meaning a bit of glitter that starts at the bottom will oscillate from bottom to top with a frequency determined by the speed of the spinning.
There will be some amount of damping from the thick liquid, so if the ball kept spinning for long enough, the glitter would end up concentrated around the equator, but it appears that the damping is small enough that the ball stops spinning long before that happens.
Thanks, Amy! It's a great thing to have for a fidgeter like me...
It's a rubber ball filled with a thick liquid, some glitter, and a smaller ball containing some LEDs and an accelerometer. When the accelerometer detects that the ball has bounced, it starts blinking the LEDs for a few seconds. I've found that a quick wrist-flick can also trigger them. What I'd like to talk about here though is what happens when the ball spins:
I would have expected the glitter to tend toward the widest part of the ball, the center, but instead it fills the whole thing.
We'll assume that the thick liquid makes the force of gravity negligible, much like in the Neutral Buoyancy Laboratory used by NASA. That just leaves the normal force that the sides of the ball apply to the glitter. The radial component of this force will be related to the rotation of the ball by
where m is the mass of the glitter, r is the radius of the ball at a particular height, ω is the angular velocity of the ball's rotation, and N is the normal force. Since the ball is spherical, we can express r in terms of the height, z:
where R is the radius of the ball at its center. Using this, we can express the slope of the wall in terms of z as well:
This gives the direction of the normal force as
so putting this into our original equation and solving for N gives
Now that we have a general equation for N, we can find its z component:
Since we're assuming that the normal force is the only force on the glitter, we can write
Solving this differential equation with the initial condition z(0) = z'(0) = 0 gives
meaning a bit of glitter that starts at the bottom will oscillate from bottom to top with a frequency determined by the speed of the spinning.
There will be some amount of damping from the thick liquid, so if the ball kept spinning for long enough, the glitter would end up concentrated around the equator, but it appears that the damping is small enough that the ball stops spinning long before that happens.
Thanks, Amy! It's a great thing to have for a fidgeter like me...
Wednesday, July 6, 2011
Propeller Head
The other day on the highway, we passed a trailer carrying a motorboat with two outboard motors on it: one with a very small propeller, and the other with a larger one. It made me wonder how the two would behave differently – a larger propeller clearly would give more thrust, but would also require more power. Do the two cancel each other out?
We can find the forward force on the boat by relating it to the change in momentum of the water:
where m is the mass of water accelerated, Δv is its change in velocity, and Δt is the time it takes to accomplish the acceleration. Normally, this should be a differential, but we're only interested in the average force, so we can treat it as a difference quotient. Let's define some parameters for each propeller:
The blue circle represents the rotation of the propeller at an angular velocity ω, or with period p. The red circle represents the angle the blades are twisted to, θ. The length of the blades is r, and their apparent width, as viewed from the side, is w. Using all this, we can rewrite the force as
where n is the number of blades, and ρ is the density of water.
Next, we want to figure out the power required to turn the blades. We'll use a similar technique to the above, but this time using torque and angular momentum. The water will be accelerated to a velocity given by
That means at a radius a, the water will have an angular momentum of
or resolving the cross product,
To get the total angular momentum, we integrate over all radii:
As with the force above, we can express the torque as a change in angular momentum:
And from this, we can find the power output of the motor:
Interestingly, this means that both the power required and the force obtained are proportional to r/p. The implication then is that the size of the propeller doesn't matter — a smaller one needs to move faster, but it's easier. I'm not sure why one size might be preferable to another, but it may have to do with the amount of noise or wake created.
We can find the forward force on the boat by relating it to the change in momentum of the water:
where m is the mass of water accelerated, Δv is its change in velocity, and Δt is the time it takes to accomplish the acceleration. Normally, this should be a differential, but we're only interested in the average force, so we can treat it as a difference quotient. Let's define some parameters for each propeller:
The blue circle represents the rotation of the propeller at an angular velocity ω, or with period p. The red circle represents the angle the blades are twisted to, θ. The length of the blades is r, and their apparent width, as viewed from the side, is w. Using all this, we can rewrite the force as
where n is the number of blades, and ρ is the density of water.
Next, we want to figure out the power required to turn the blades. We'll use a similar technique to the above, but this time using torque and angular momentum. The water will be accelerated to a velocity given by
That means at a radius a, the water will have an angular momentum of
or resolving the cross product,
To get the total angular momentum, we integrate over all radii:
As with the force above, we can express the torque as a change in angular momentum:
And from this, we can find the power output of the motor:
Interestingly, this means that both the power required and the force obtained are proportional to r/p. The implication then is that the size of the propeller doesn't matter — a smaller one needs to move faster, but it's easier. I'm not sure why one size might be preferable to another, but it may have to do with the amount of noise or wake created.
Subscribe to:
Comments (Atom)