Through my many, many physics classes, I've never done much with fluid mechanics, and I've often thought of questions about how such systems work. Recently I was thinking about
Archimedes' principle, which is behind the famous exclamation of "Eureka!" and I wondered whether I could derive it using the physics that I do know.
The principle states that an object placed in water (or other fluid) will displace a volume of equal mass. The way I thought about this was that the displaced water has to go on top of the water surrounding the object. This increases the potential energy of the water, since
where
m is the mass,
g is the acceleration due to gravity, and
h is the height. Lowering the object decreases its energy, but pushes more water up, increasing that energy. I figured I could map out the energy of the system by placing an object at a given height, filling a set volume of water around it, then measuring the energy using the equation above. To start with, I tried a simple box, with a density 90% that of water:
Plots of gravitational potential energy are really handy, since you can think of them like a hill: an object will roll down to the lowest point. The knee in this graph shows where the box floats, and the different slopes on either side show that it's easier to push the box further into the water than to lift it out.
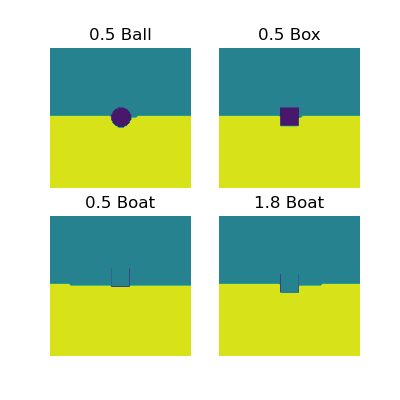
The box is the simplest case, since it's easy to calculate the amount of water displaced, but I was curious to try the same method on more complicated shapes, specifically a ball and a boat, which I approximated as a hollow box:
These plots show the grid of water/air/object I made to calculate the energy. The labels give the fractional density of the object that I used. Since the boat is just a thin frame filled with air, the frame can be much denser than water and still float. If you look carefully at the border between the air and water, you can see a wrinkle – This is due to the resolution of the grid I used. The water is not able to spread perfectly evenly.
Now to Archimedes: For the various cases above, we can measure the displaced volume of water by counting the cells below the water level that belong to the object or air. We can compare that to the total weight of the object – Count its cells and multiply by its density. We can do that for each of the 3 shapes, and vary the size and density:
Aside from a bit of error from the wrinkles I mentioned, the points fall on the line, just as Archimedes predicted! This is
one case where considering energy did make things easier.
